前言
比特币的历史报酬率在机率上如何分布一直是一个值得争论的话题,特别是这类的统计机率分配被应用在许多金融资产订价及分析的同时,比特币又是一个极为特殊的存在。这篇文章将简单介绍关于 BTC 历史报酬率机率分布的意义以及相关研究方式与结果。
何谓常态分配
在介绍今天的话题时,务必先简介常态分布的定义。常态分配,又被称为高斯分配或正态分配,是统计学中一种常见的概率分配。它在自然界和许多社会现象中都具有重要的应用。常态分配的特点是对称且呈钟形曲线,其机率密度函数具有以下该图形式。
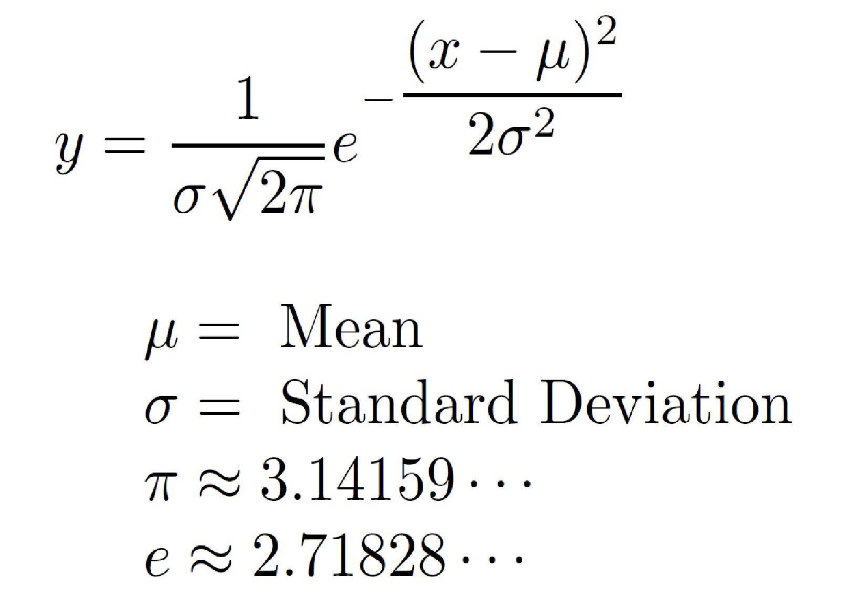
μ 表示平均值,σ 表示标准差,e 表示自然对数的底数。
常态分配的平均值(μ)代表分布的中心位置,标准差(σ)则代表分布的变异性。根据常态分配的性质,约有 68% 的数据落在平均值加减一个标准差的范围内,约有 95% 的数据落在平均值加减两个标准差的范围内,约有 99.7% 的数据落在平均值加减三个标准差的范围内。这三组数字相信读者们在国高中的数学课上多少都会有印象,此即所谓的经验法则(Empirical Rule )
 利用预期的概念简单理解常态分配
利用预期的概念简单理解常态分配
总上所述,由于常态分配的性质和广泛的应用,许多自然和社会现象都可以近似被视为常态分布。例如人的身高、体重和智力测验通常遵循常态分布,并且对于理解和分析各种现象的变异性具有重要意义。
常态分配对金融资产及 BTC 的意义
在传统金融领域,许多实证研究发现股票市场的日回报和利率的变动被认为是近似于常态分布的,然而常态分配对于 BTC 及各类金融资产还有许多意义,我稍微统整了三大点。
❶波动性预测:常态分配可以用来描述金融资产和 BTC 的波动性。通常,波动性是指资产价格的变动幅度。如标准差或波动率,这些指标能帮助评估风险和制定交易策略。
❷统计分析:金融资产和 BTC 的收益率通常被假设为服从常态分配。在进行统计分析时,这种假设可以用于计算信心区间、假设检验和相关统计量等。例如,可以使用常态分配来计算投资组合的预期收益率和风险,或者进行交易策略的回测和模拟。
❸随机模拟:基于常态分配的随机模拟可以用于金融风险管理和投资评估。通过生成符合常态分布的随机数据,可以模拟不同市场情境下资产价格的变动,从而评估投资组合的价值和风险。
BTC的历史报酬率
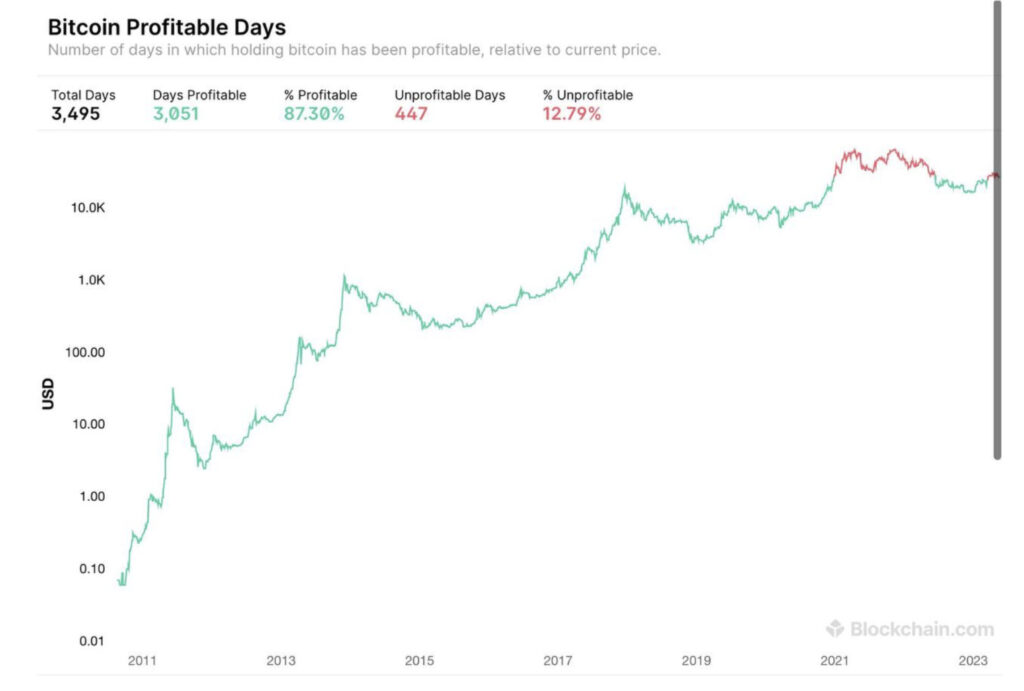
上图为 BTC 自 2011 年起的盈利天数,在将近 3500 天中,高达 87.3 % 呈现盈利状态。若是单看这张图可能会觉得 BTC 在历史日报酬的机率分配上会不太均匀,因此有人将 BTC 的价格资料转换成机率分配图,形成下图的分配状态。一项有趣的发现是,BTC 的长期报酬率看似美好,但日报酬率却只有区区 0.2%,侧面显示了 Daytrading 的难度与长期持有的复利幅度。
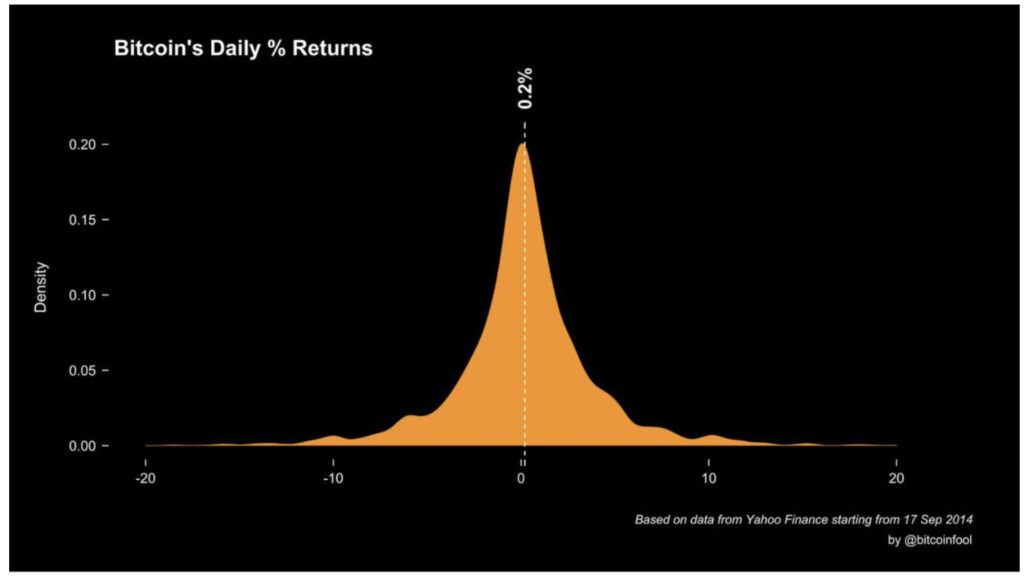
附注:该图的转换方式(参考 @bitcoinfool)
①下载 Yahoo Finance BTC 价格资料
②使用 R 语言的 DPLYR 套件添加新变量
③使用 ggplot 绘制直方图
④于 Rhino 中调整图形
更深入的研究方式
在前述的内容介绍了常态分配的概念以及其对 BTC历史报酬率的意义,不过在机率分配上,其实有更适合的分配模式适合 BTC 这类特殊的金融资产。
接下来的内容将参考 Swan Capital 的《Examining Historical Returns and Volatility in Bitcoin》一短论文进行更详细的说明。
什么样的机率分配才最适合 BTC 历史回报率?
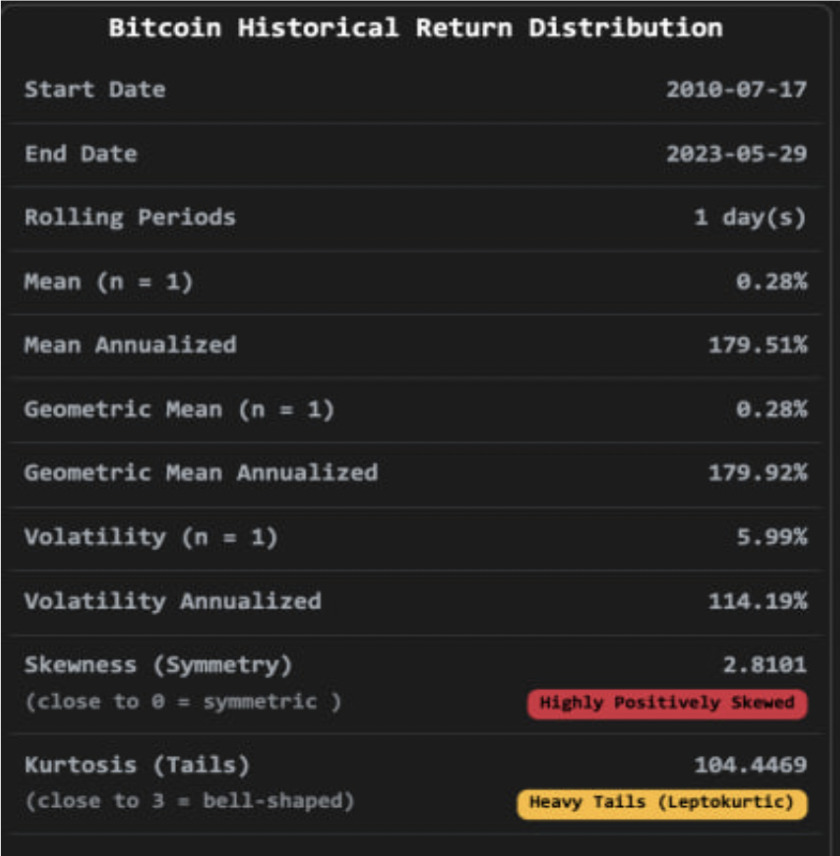
经过该团队分析2010 – 2023 年的价格数据,BTC 的历史报酬率是不适合用常态分布来呈现的,与我们上述的股票日报酬率及利率的变动有所差别。原因在于比特币报酬率的偏态量数(skewness ) 与峰态量数( kurtosis )
简单来说,偏态量数是用来观察资料分布是否对称,而峰态量数则可以观察资料分布是否具有厚尾,即是否有离群值。如下图显示,BTC Return 的偏态量数达到 2.8 左右,显著偏离对称性的 0,而峰态量数高达 104,离常态分布(bell shaped ) 的 3 偏离非常多,代表有许多离群值影响,这边也不难联想到 BTC 的高波动性造成的报酬率变动。( Ex : 如2023 的 Q1涨幅)
而对比 S&P500 指数的长期报酬分布来看,偏度大约为 -0.3,峰度为 10,显示了分布更对称、离群值更少的稳定市场。
该团队认为最适合的机率分配为 generalized hyperbolic(广义双曲线分布),这是一种可以呈现各式机率分布形状的模式,意思是不需要对称也能处理,并且还能有效表现出离群值数据,很适合使用在许多金融产品身上。对于我们一般投资人而言,势必只需要了解它的重要性何在即可,不需要过度纠结背后原理。
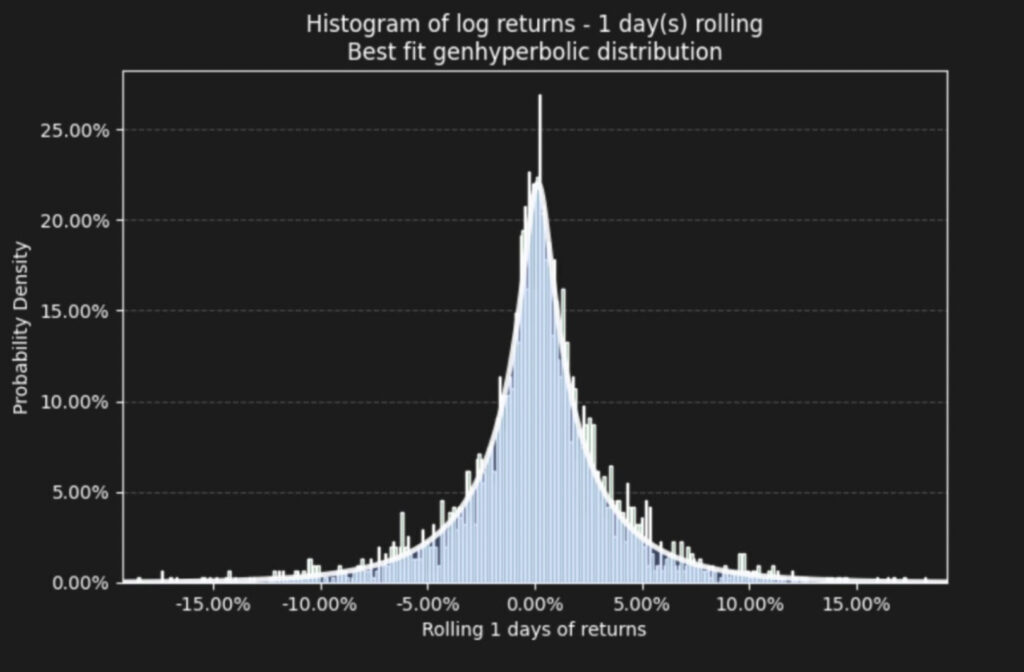
广义双曲线分布在 BTC 报酬分布上呈现的结果
理解 BTC 报酬率的分布有什么样的用意?
接下来是本篇文章中最主要的部分,在理解完 BTC 报酬率的机率分布后,最重要的就是能够进行蒙地卡罗模拟(Monte Carlo simulation)
蒙地卡罗模拟是一种统计模拟方法,通过随机抽样和重覆实验来估计未来事件的机率和可能的结果。在金融领域,蒙地卡罗模拟常用于模拟投资组合、期权定价、风险评估等问题,而这边的研究方向自然是针对 BTC 的价格走势及可能价值做估计。以下我统整了针对 BTC 报酬率进行蒙地卡罗模拟的六步骤,让读者们感受大致的框架与逻辑。
❶收集历史数据:收集 BTC 的历史价格数据,包括每日或每月的收盘价。
❷计算报酬率:根据历史价格数据,计算每个时间段的报酬率。
❸建立模型:基于历史报酬率数据,建立一个统计模型来描述 BTC 的未来报酬率分布。
❹设定参数:根据模型的参数,设定模拟的时间范围和模拟次数。时间范围可以是未来的若干天、月或年,模拟次数越多,结果越准确。
❺进行模拟:使用设定的模型和参数,进行蒙特卡罗模拟,生成大量的随机路径,模拟未来的 BTC 报酬率走势。
❻分析结果:根据模拟生成的数据,可以对未来的 BTC 报酬率进行统计分析,计算期望收益率、风险指标(如标准差、价值 -at-Risk 等),或者绘制报酬率的概率分布图等。
聪明的读者们可能也能发现,前面建构出来的机率分布就是为了第三步骤的模型建立,这也会是整个模拟的关键之一。而我也透过工具进行了一次蒙地卡罗模拟,稍加设定参数后,对于 BTC 未来一年的价格认为会达到 5.5 万美元左右的水准,供各位参考。
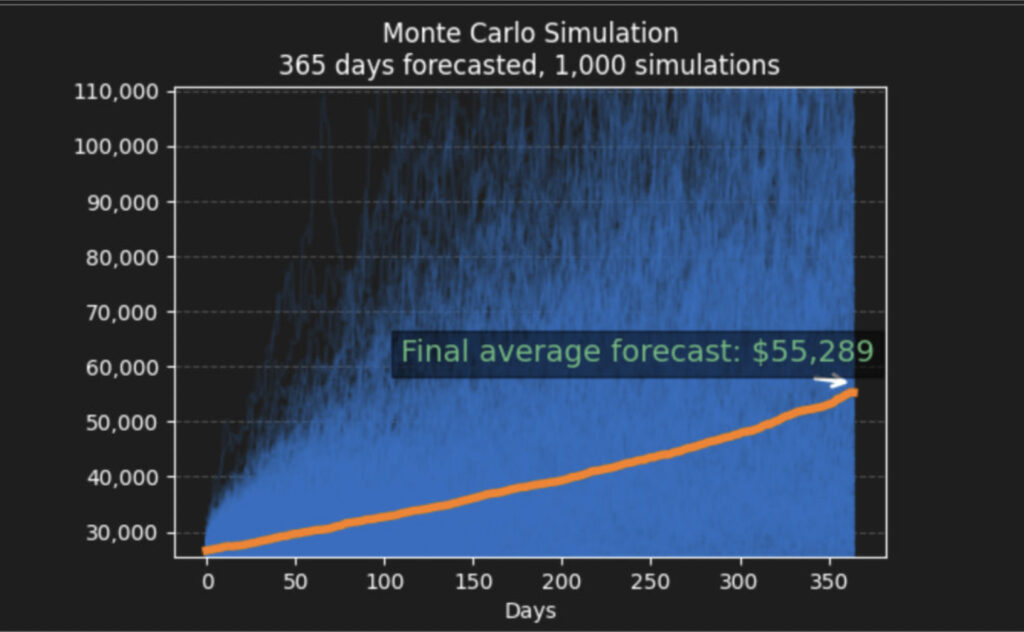
蒙地卡罗模拟结果
额外特殊发现
该团队也发现,采用 GARCH 模型对BTC 报酬率进行测试,会有 autocorrelation 的现象,简单理解就是 BTC 过去的报酬是会确切影响未来的,这一点是很多估值模型会忽略的部分。
附注:
GARCH 模型是指广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroskedasticity Model)。它是一种用于分析时间序列数据中波动性变化的经济计量模型,用于描述金融市场中资产价格和指数的波动性变化。
自相关性(Autocorrelation)是指一个时间序列变量与其自身在不同时间点上的相关性。在统计学和时间序列分析中,自相关性是衡量时间序列数据中观测值之间的依赖关系和相关性强度的指标。
结论
比特币一直以来都是一个极为特殊的金融资产,有着高度的变化,却也走出自己独特的样貌。一般的投资者可能也不曾思考及研究过这类透过机率分布及模拟进行估值的方式。希望透过这篇文章让各位读者有初步的了解及体验。
还是需要强调,市场上会有这么多的估值模型,就是因为没有一个是准的。因此谨慎且开放性的思考才是最重要的关键,切勿过度执着。
另外本篇涉及了不少计量统计学的知识,在撰文过程中已尽可能使用较白话的方式说明,并且有蛮多专有名词翻译上可能也有疏漏(太多都是原文书上的名词定义)若有误述或是表达不清楚的部分欢迎与我联系。
TG : @MingYang0901
完整论文连结:Bitcoin Historical Returns Analysis (nakamotoportfolio.com)
模型程式码开源:https://github.com/pxsocs/nakamoto_code/blob/main/bitcoin_distribution.ipynb
学习讨论群组
那以上所有的分析方法/资料分享可以在哪里 学习/看到 呢!
除了网路上有许多免费/付费学习资源以外,推荐你们加入DA Capital 的附属组织DA Trader Association 的讨论群组一起讨论喔!
只要动动你的小手,使用DATA 网站上的邀请码就能够加入「VIP」群组,获得高质量的学习资源喔!
里面注重各个面向的发展与学习或是等待接下来2023/Q2 要释出的课程!
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




