Author: Stone, B² Network Research Lead

B² Network is a Layer2 solution on Bitcoin, mainly utilizing the submission of zero-knowledge proof verification commitments to the Bitcoin network, allowing challengers to initiate fraud proofs to ensure the security of B² Network by leveraging the strong consensus of the Bitcoin network.

This article mainly introduces the operation mechanism of ZK-Rollup and OP-Rollup on Ethereum, introduces the magical NAND gate circuit, introduces the role of commitments, and designs the zero-knowledge proof verification commitment on B² Network using these mechanisms and concepts, and then explains how zero-knowledge proof verification commitments are executed on the Bitcoin network and how the security of B² Network is ensured.

ZK-Rollup on Ethereum

ZK-Rollup is a Layer2 scaling solution for blockchain, which aggregates multiple transactions and uses zero-knowledge proofs to ensure the correctness and integrity of these transaction batches, and verifies the zero-knowledge proofs on the first-layer blockchain network to ensure the security of the second-layer network. It aims to increase the throughput of the blockchain system, reduce transaction fees, and maintain a high level of security and data integrity.

The operation process of ZK-Rollup is roughly as follows:

1. Transaction aggregation and sorting. Users submit transactions to ZK-Rollup, and the transactions will be submitted to the mempool. ZK-Rollup's Sequencer retrieves users' transactions from the mempool, collects and sorts them, and is responsible for processing transactions, updating account states, and ultimately generating a batch representing these updates.

2. State transition and computation. All transaction execution and state updates are performed off-chain. ZK-Rollup's VM (including different zero-knowledge proof smart contract execution engines such as zkEVM, zkVM, etc.) calculates the new account state and processes operations such as transfers, smart contract interactions, etc. It also generates the necessary data and evidence to prove that these transactions and state updates are valid, including the new account state and zero-knowledge proof.

3. Zero-knowledge proof generation. ZK-Rollup's Prover uses zero-knowledge proof technology (such as zk-SNARKs or zk-STARKs) to create a proof that all aggregated transactions are valid and do not violate network rules. This proof does not reveal any information about the transaction content, protecting user privacy while ensuring data integrity and security.

4. Zero-knowledge proof verification. The Aggregator submits the batch data and zero-knowledge proof to the first-layer blockchain network. This usually occurs in a compressed form to reduce the required on-chain space. Smart contracts on the first-layer blockchain network receive this data and proof and verify the validity of the proof. If the proof is valid, the contract will update the state of the ZK-Rollup layer it records.

The core of ZK-Rollup lies in the generation and verification of zero-knowledge proofs. ZK-Rollup's transactions are executed off-chain, and the state is generated off-chain. Prover generates zero-knowledge proofs as commitments for ZK-Rollup. These commitments represent that the transactions on ZK-Rollup are executed correctly and effectively, generating the correct state. The first-layer blockchain network does not need to verify all transactions and states of ZK-Rollup, only the commitments need to be verified. The verification of commitments is done through zero-knowledge proof verification by the smart contract of the first-layer network, confirming the validity of ZK-Rollup.

Therefore, in Ethereum's ZK-Rollup, zero-knowledge proof data is the commitment submitted by the second-layer network to the first-layer network.

OP-Rollup on Ethereum

Optimistic Rollup (OP-Rollup) is a technology designed to scale blockchain performance by maintaining minimal data on-chain and performing as many computations as possible off-chain. OP-Rollup utilizes an "optimistic" assumption, assuming that most transactions are honest, and does not immediately verify the validity of each transaction, greatly increasing throughput and efficiency.

The operation process of OP-Rollup is roughly as follows:

1. Transaction aggregation and sorting. Users submit transactions to OP-Rollup, and the transactions will be submitted to the mempool. OP-Rollup's Sequencer retrieves users' transactions from the mempool, collects and sorts them, and is responsible for processing transactions, updating account states, and ultimately generating a batch representing these updates.

2. Transaction execution. Transactions on OP-Rollup are executed off-chain. The execution of each batch of transactions will transform the old state into a new state, and each batch will calculate a new state root (an encrypted "snapshot" representing the entire system state) and submit it to the first-layer blockchain network.

3. State verification. OP-Rollup does not immediately perform complex verification when submitting transaction batches, but "optimistically" assumes that these transactions are valid and then submits them to the first-layer blockchain network. If observers believe that a batch is invalid, they can submit a fraud proof to challenge the batch. In the Optimistic Rollup solution, fraud proof is a mechanism that allows any observer to challenge erroneous or maliciously submitted states or transactions. Optimistic Rollup uses fraud proofs to ensure that even "optimistically" accepted transactions can be proven wrong afterwards and accordingly revoked.

4. Challenge mechanism. After the confirmation of the state submission by OP-Rollup, there is a challenge window during which anyone can check the submitted batch and submit a fraud proof when an error is found. This is usually achieved by submitting a transaction to the first-layer blockchain network, declaring the error they believe and providing the corresponding evidence. Arbitrum Rollup (a solution of Optimistic Rollup) uses a process called "interactive verification game" to address challenges. In this process, challengers and submitters engage in a series of rounds to gradually narrow down the range of disagreement on where the error occurred (using binary search to quickly locate the position of the error). Ultimately, this process will determine the exact location of the error. Once the error is confirmed, the original batch will be revoked, and the validator who raised the error will be penalized. If the challenge fails, the challenger may lose the funds they staked to initiate the challenge; if the challenge succeeds, the challenger may receive the reward for successfully initiating the challenge.

The core of OP-Rollup lies in fraud proofs and challenge mechanisms. OP-Rollup first "optimistically" confirms and submits commitments, then uses the challenge mechanism to allow anyone to challenge the submitted commitments, ultimately ensuring the verification and confirmation of OP-Rollup through commitments and challenges.

Magical NAND Gate

The NAND gate is a basic logic gate in digital logic, which implements the logical NOT operation after the logical AND operation. The characteristics of the NAND gate make it the basis for constructing any other logic gates and complex logic circuits. Here is a detailed introduction on how to use the NAND gate to construct logic gates (such as AND gate, OR gate, XOR gate), as well as addition and subtraction gates:

1. Basic NAND Gate

The NAND gate has two inputs, and the output is 0 only when both inputs are 1; in all other cases, the output is 1. This can be expressed as A NAND B in logical expression.

2. Constructing Basic Logic Gates

AND Gate

To construct an AND gate using NAND gates:

• Step 1: Connect the two inputs to a NAND gate.

• Step 2: Connect the output of this NAND gate to the two input terminals of another NAND gate.

• Result: The output of the second NAND gate is the result of the AND gate.

OR Gate

To construct an OR gate using NAND gates:

• Step 1: Pass each input through a NAND gate (each input connected to itself), producing the effect of two NOT gates.

• Step 2: Use the outputs of these two NAND gates as inputs to another NAND gate.

• Result: The output of this NAND gate is the result of the OR gate.

XOR Gate

To construct an XOR gate using NAND gates (more complex):

• Step 1: Construct two NAND gates, with each input connected to one of them.

• Step 2: Use the outputs of the two NAND gates from step 1 as inputs to a third NAND gate.

• Step 3: Connect the original inputs A and B to a fourth NAND gate, and connect the original input B and the output of the second NAND gate to a fifth NAND gate.

• Step 4: Finally, connect the outputs of the fourth and fifth NAND gates to a sixth NAND gate.

• Result: The output of the sixth NAND gate is the result of the XOR gate.

3. Constructing Addition Gates

Half Adder

A half adder is a simple adder that can handle addition of two bits and produce a sum and carry.

• Sum: Use an XOR gate to generate the sum.

• Carry: Use an AND gate to generate the carry.

• Construct these basic gates using NAND gates, and then combine them to form a half adder.

Full Adder

A full adder considers carry input from the low bit.

• Step 1: Construct two half adders, with the first handling A and B, and the second handling the sum from the first half adder and carry input C.

• Sum: Output of the second half adder.

• Carry: Connect the carry outputs of the two half adders with an OR gate.

• Construct half adders and an OR gate using NAND gates, and then combine them to form a full adder.

4. Constructing Subtraction Gates

Half Subtractor

A half subtractor handles subtraction of two bits.

• Difference: Use an XOR gate to generate the difference.

• Borrow: Use a NAND gate and a NOT gate to generate the borrow.

• Construct an XOR gate and other required logic using NAND gates, and then combine them to form a half subtractor.

Full Subtractor

A full subtractor considers borrow input from the high bit.

• Step 1: Construct two half subtractors, with the first handling A and B, and the second handling the difference from the first half subtractor and borrow input.

• Difference: Output of the second half subtractor.

• Borrow: Connect the borrow outputs of the two half subtractors with an OR gate.

• Construct half subtractors and an OR gate using NAND gates, and then combine them to form a full subtractor.

5. Constructing Multiplication Gates

Binary Multiplication

Implement multiplication of two binary numbers.

• Step 1: Use AND gates for bit multiplication.

• Step 2: Use full adders in series for continuous addition.

• Step 3: Implement shifting and accumulation.

6. Constructing Registers

D Flip-Flop

Stores a single bit of binary information.

• Step 1: Create a latch using NAND gates.

• Step 2: Extend the latch to a flip-flop.

Registers

Stores multiple bits of binary numbers.

• Connect multiple D flip-flops in parallel, with each storing one bit.

7. Constructing Clocks

Oscillator

Provides periodic clock signals.

• Create a feedback loop using NAND gates to generate continuous oscillation.

Conclusion

The NAND gate is called the "universal logic gate" because of its ability to construct any other logic gate and complex circuits. Using the above methods, complex addition, subtraction, multiplication, as well as storage and clock circuits can be constructed using NAND gates, forming the basis for arithmetic operations in computers and digital systems. In modern integrated circuit design, the NAND gate is widely used due to its simplicity and versatility.

In the practice of B² Network, any computing logic can be constructed using NAND gates.

Commitment in Cryptography

Commitments are widely used in cryptography and blockchain, such as SHA256, Merkle Tree, and KZG in zero-knowledge proofs. As mentioned earlier, ZK-Rollup uses zero-knowledge proofs as commitments, and OP-Rollup uses bytecode from the virtual machine as commitments.

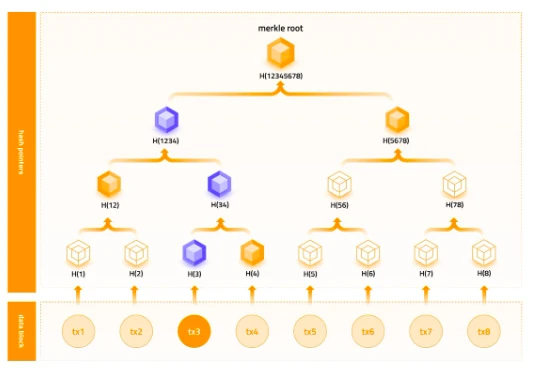
Let's explain how commitments are used through Merkle Tree:

1. Commit: The Prover calculates the hash of all values, and the hash becomes the leaf node of the binary tree. Hash calculations are performed upwards to generate the Merkle Tree, and the root hash of the tree is published as the commitment.

2. Reveal: The Prover reveals a value corresponding to a leaf node, along with its branch.

3. Check: The Verifier calculates the hash using the revealed value and branch, and compares it with the published commitment for verification.

The example below illustrates this process:

1. Commit: The Prover calculates the hash of tx1, tx2, …, tx8, obtaining H(1), H(2), …, H(8). Hash calculations are performed pairwise to generate the binary tree structure, i.e., the Merkle Tree. The root node's value H(12345678) is published as the commitment.

2. Reveal: The Prover reveals a value, such as tx3, and its branch (H(4) -> H(12) -> H(5678)).

3. Check: The Verifier calculates and verifies the commitment using the revealed tx3 and branch (H(4) -> H(12) -> H(5678)):

   • Calculate the hash of tx3, H(3)
   • Hash H(3) with H(4) from the branch to get H(34)
   • Hash H(34) with H(12) from the branch to get H(1234)
   • Hash H(1234) with H(5678) from the branch to get H(12345678)
   • Verify H(12345678) with the published commitment

Zero-Knowledge Proof Verification Commitment in B² Network

B² Network is a second-layer solution based on Bitcoin network's ZK-Rollup.

Limitations of ZK-Rollup on Bitcoin

Due to the Turing incomplete limitation of Bitcoin, it is not possible to perform zero-knowledge proof verification on the Bitcoin network. Therefore, the traditional implementation of ZK-Rollup, which verifies zero-knowledge proofs on the first-layer blockchain network, cannot be achieved on the Bitcoin network.

ZK-Rollup only aggregates zero-knowledge proofs and Rollup data through Taproot into the Bitcoin network, ensuring that the ZK-Rollup data is anchored in the Bitcoin network and cannot be tampered with. However, it cannot guarantee the validity and correctness of ZK-Rollup transactions, nor can it leverage the strong consensus of the Bitcoin network to ensure the security of the second-layer ZK-Rollup.

Therefore, it is necessary to confirm ZK-Rollup on the Bitcoin network.

Zero-Knowledge Proof and Arithmetic Circuits

Zero-Knowledge Proof

In zero-knowledge proofs, arithmetic circuits are used to construct a proof where the prover knows certain secret information without revealing the information itself.

Zero-knowledge proofs use arithmetic circuits to generate a proof:

• Generating a Proof Once the arithmetic circuit is established, the prover uses their secret inputs to calculate the circuit's output. During this process, the prover also generates additional information (such as commitments and random numbers specific to zero-knowledge proofs) used to construct the proof.

• Verifying the Proof The prover sends their proof to the verifier. The verifier does not know the prover's secret inputs, but they have the circuit's description and the prover's proof. The verifier validates the proof by performing the same calculation as the circuit and comparing the results with the proof provided by the prover.

Arithmetic Circuits

Arithmetic circuits are typically represented as a directed acyclic graph (DAG), where each node represents an arithmetic operation and edges represent the flow of data between operations. Input nodes represent the circuit's input values, usually some numbers or variables, while internal nodes represent arithmetic operations. The circuit's output is the final computed result.

Basic circuit gates in arithmetic circuits include:

• Addition Gates
• Multiplication Gates

As mentioned in the previous section on NAND gates, arithmetic circuits can be transformed into logic gate circuits based on NAND gates by converting addition gates and multiplication gates into NAND gates.

Zero-Knowledge Proof Verification Commitment

The verification process of zero-knowledge proofs itself is an arithmetic circuit. By transforming the arithmetic circuit into a logic gate circuit based on NAND gates, the verification process of zero-knowledge proofs can be transformed into a logic gate circuit based on NAND gates.

NAND gates are implemented through Bitcoin scripts, assembling Bit Value Commitments as inputs and outputs into logic gates to enforce logic gate constraints.

This can be summarized as hashc0 > hashc1 > hashb0 > hashb1 > hasha0 > hasha1 > OPGATECOMMITMENT, with the corresponding unlocking script preimagea > preimageb > preimagec.

In practice, it is possible to implement NAND gates through Bitcoin scripts, then construct addition gates and multiplication gates from NAND gates, combine them to form an arithmetic circuit, and ultimately construct the verification program for zero-knowledge proofs. However, due to the large number of gate circuits involved, the resulting Bitcoin script would be very large and impractical to run on the Bitcoin network.

By assembling Bit Value Commitments as inputs and outputs into logic gates, with each logic gate representing a leaf node with different inputs and outputs, and combining them into a circuit binary tree, the published Circuit Taproot is the root of the binary tree, reducing the size of the publication.

Circuit Taproot serves as the commitment submitted by B² Rollup on the first-layer blockchain network, Bitcoin. Unlike traditional ZK-Rollup, which can perform verification on the first-layer network, B² Rollup cannot directly perform verification on Bitcoin. However, it can provide a challenge mechanism for the commitment, similar to the approach of Optimistic Rollup, to confirm the Circuit Taproot commitment.

Verification and Response Protocol

Unlike BitVM, which requires pre-signing of off-chain transactions between two parties, B² Network uses UTXO transactions with locked rewards, and the unlocking script is a Taproot script.

The specific unlocking Taproot script is prepared in advance by the Prover for each branch of the Circuit Taproot Tree, along with the input hash. The Challenger uses the preimage to execute the script. If the executed output does not match the Prover's submission, the entire Taproot can be unlocked using MAST (Merkleized Abstract Syntax Tree), allowing access to the locked reward.

Since the running cost of zero-knowledge verification programs is very low and very fast, users on the Bitcoin network can act as observers of the Challenge mechanism, verifying the commitments submitted by B² Rollup. If any inconsistencies are found, a challenge can be immediately initiated.

The challenge mechanism is similar to the "interactive verification game" of Arbitrum Rollup, continuously searching for incorrectly executed logic gate calculations. To find an error among many logic gates, a binary search approach is used to execute the gate circuit Bitcoin script. The challenger who finds the error branch the fastest can unlock the locked reward UTXO on the Bitcoin network and receive the reward.

Additionally, one branch of the Taproot locking script is a time-lock script. If no successful challenges occur, the Prover will unlock the UTXO and retrieve the reward after the challenge period ends.

Conclusion

Through the Ordinals Protocol, B² Network aggregates rollup data and proofs into Tapscript, effectively ensuring the data availability of the rollup.

By recording zero-knowledge proof verification commitments on Bitcoin, B² Network allows for a challenge mechanism against commitments by any observer, inheriting the security of Bitcoin and achieving consensus on rollup data on the Bitcoin network.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。