Source: New Smart Element

Image source: Generated by Unbounded AI
Terence Tao calls for mathematicians to learn to use AI
After three weeks, Terence Tao successfully used AI tools to complete the formalization of the proof process of the polynomial Freiman-Ruzsa conjecture. He once again called on mathematicians to learn to use AI tools correctly, and netizens exclaimed: Will future mathematical papers not need to be readable by humans?
The project of using AI tools to assist in mathematical research has once again been successfully demonstrated by Terence Tao!
Three weeks ago, he published a blog post, recording the process of formalizing the proof of the polynomial Freiman-Ruzsa conjecture using Blueprint in Lean4.

Just yesterday, he excitedly announced that the Lean4 project formalizing the proof of the polynomial Freiman-Ruzsa conjecture had been successful after three weeks!
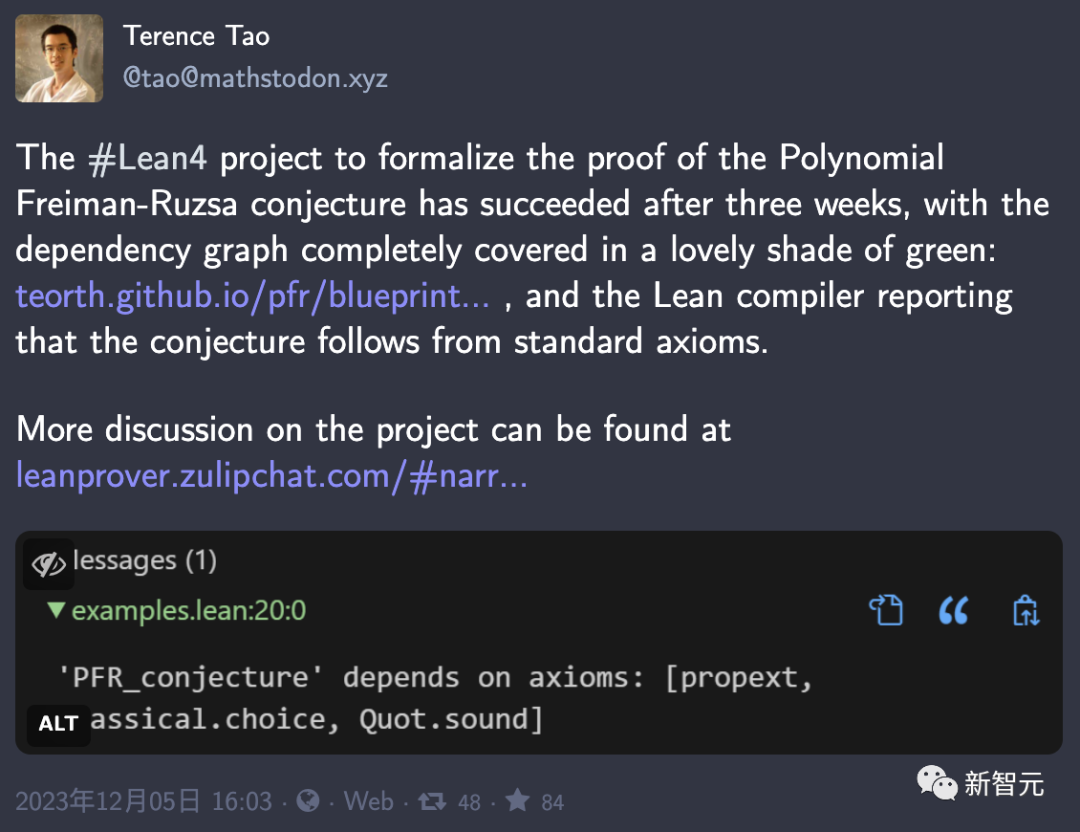
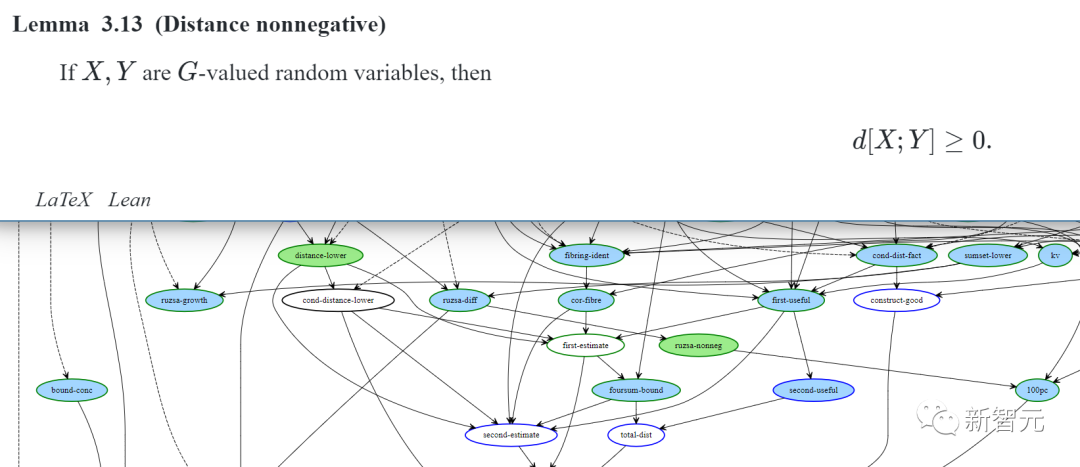
Now, the dependency graph has been completely covered in green, and the Lean compiler also reports that this conjecture fully complies with standard axioms.
Terence Tao stated that he contributed only about 5% of the code in the entire team. This result is very encouraging because it means that mathematicians can lead formalization projects in Lean even without Lean programming skills.
He found that the most interesting part in mathematics in the project was relatively easy to formalize, while the most obvious technical steps were the most time-consuming.
Breaking down the project into small to medium difficulty parts using Blueprint had a good effect, making a large amount of parallel work possible.
This way, many contributors can handle specific subtasks without needing to understand the entire proof process, or even without needing to understand relevant knowledge in the mathematical field.

Just a few minutes ago, Lean successfully proved the PFR conjecture, and did not leave any unresolved issues (referred to as "sorry" in the following text). This means that all major goals of this project have been successfully achieved.
At the same time, his blog post from three weeks ago, on November 18, was dug up by netizens, sparking heated discussions.

Sure enough, the post-revolutionary power of AI-assisted mathematical research takes months for people to realize.
Only researchers at the forefront can truly feel the impact and shock of this tremendous power in the first place.
Terence Tao calls for mathematicians to learn to use AI
A netizen asked Terence Tao: Does this mean that there are more and more proofs that are understandable by machines but not by humans?

Terence Tao stated that, on the contrary, if the formalization of proofs becomes more mainstream and receives more AI assistance, it is entirely possible to create proofs that are both readable by humans and understandable by machines.
The blueprint of the PFR proof proves this point—readable by humans, with each proof step accompanied by a formal reason, and a dependency graph to visualize the entire structure of the argument.

Of course, Terence Tao also cautioned against confusing "computer-assisted proof" with "proofs that cannot provide understanding/accidentally hold true."
For example, for the proof of the classification of finite simple groups, which exceeds 10,000 pages, almost 100% was generated by humans, but an alternative proof assisted by a computer is more satisfying in some respects.

After several rounds of discussion with netizens, Terence Tao made the following conclusion—
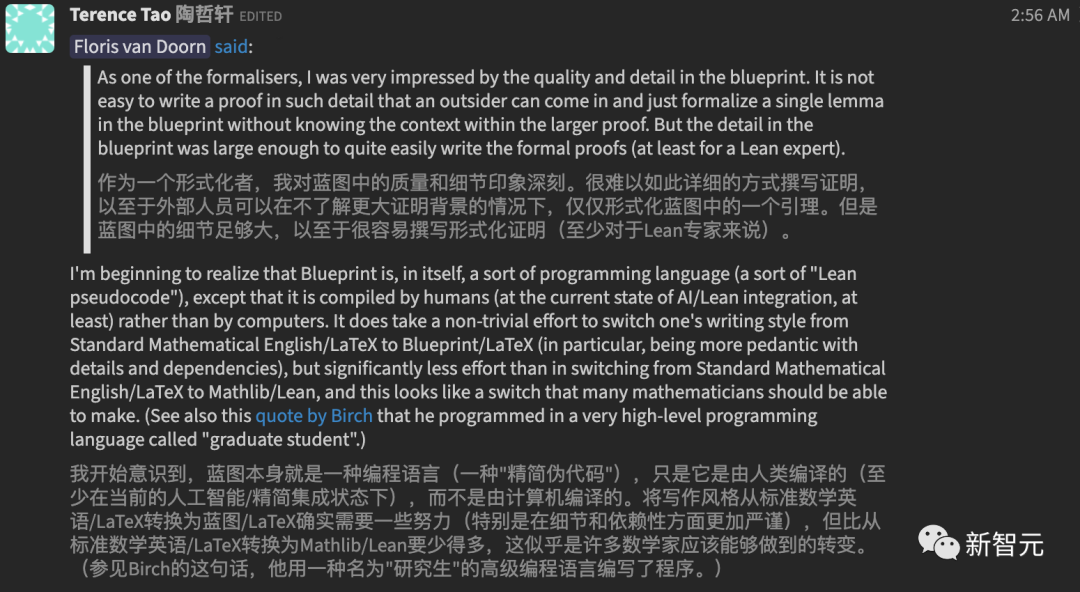
Blueprint itself is a kind of programming language and can be seen as a pseudocode for Lean.
Many mathematicians should change their writing style from standard mathematical English/LaTeX to Blueprint/LaTeX.
Netizen: In the future, research doesn't need to be "readable by humans," AI just needs to understand it
Netizens expressed that Terence Tao's mastery of various research tools is almost terrifying.
My attempt at mathematics during my graduate studies was like a caveman trying to ride a regular unicycle, and suddenly a helicopter appeared in front of me, with someone on it reaching out their hand, telling me to give it a try, and it's not scary at all.
Since I heard about the four-color theorem, I have been very clear that formalization is the future of mathematics. But what I didn't anticipate is that, as formalization is just beginning to gain traction in mainstream mathematics, Terence Tao can use AI to complete almost all mathematical writing.

Formalization refers to truly deriving each statement in the proof from basic axioms and rules. In this blog post, Terence Tao abstracted the labor of rote memorization and handed it over to the machine.
His work shows that formalization is just beginning to receive attention in mainstream mathematics.

Here is the translation of the provided markdown:
Someone has already begun to imagine: it is very likely that there will come a time when most proofs are only completed in Lean or similar systems, and no one will need to bother writing a "human-readable" paper anymore.
Mathematics will become a form of programming!

A mathematics master's student stated that their research process now consists of three steps:
- Understanding what they want to prove, through reading or discussions with others;
- Sketching out the key points on paper;
- Inputting the draft into LaTeX to make their work readable by humans.

Yes, if we are just training or fine-tuning AI to produce answers, and then writing a loop to provide feedback until the compiler outputs correctly, then we ourselves do not really need to understand.
With this method, we can also generate more training examples, manually check if the results meet the requirements, and make annotations. Training can improve the accuracy of the initial answers.

Formalization process of the PFR conjecture
Below is the formalization process posted by Terence Tao on his blog, and interested readers can give it a try.
In November, Terence Tao, along with Yael Dillies and Bhavik Mehta, initiated a collaborative project to formalize their preprint paper on the Freiman-Ruzsa (PFR) conjecture using Lean4.
Although the project had been running for less than a week, progress was quite smooth, and most of the files had been formalized.
This project benefited from Patrick Massot's Blueprint tool, which allowed the team to write "blueprints" of proofs closely related to Lean formalization and readable by humans.
In Blueprint, there is a feature that Terence Tao particularly likes, which is the automatically generated dependency graph. It provides a rough snapshot of the formalization progress. At that time, the dependency graph looked like this:
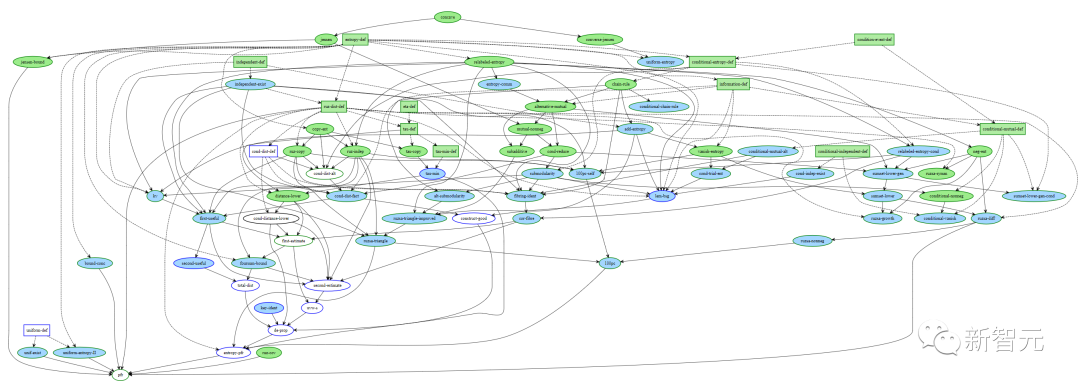
In the legend of the dependency graph, different bubbles (representing lemmas) and rectangles (representing definitions) are assigned different colors.
In simple terms, green bubbles or rectangles represent lemmas or definitions that have been fully formalized, while blue ones indicate lemmas or definitions that are ready for formalization (meaning their statements have been formalized, but the proofs have not, and the same goes for all relevant prerequisite lemmas and proofs).
The goal of Terence Tao's team is to turn all the bottom bubbles leading to the "pfr" bubble into green.
Clicking on the "pfr" bubble at the bottom of the dependency graph reveals the following content:
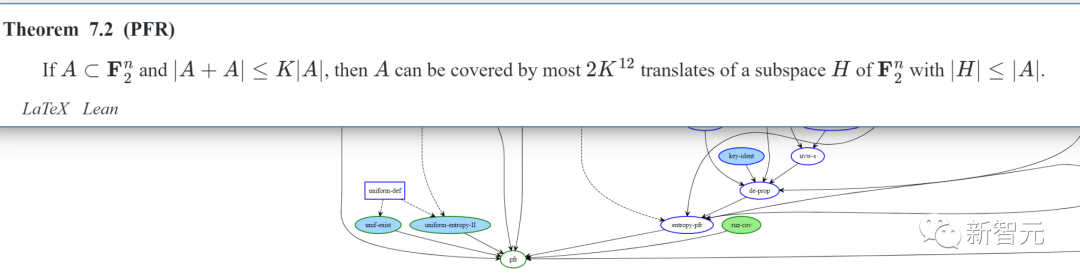
In the image, Blueprint displays a human-readable form of the PFR statement, along with a human-readable proof of the statement, which depends on other statements in the project:

Note that the "pfr" bubble is white but has a green border, indicating that the statement of PFR has been formalized in Lean, but the proof has not.
The proof itself is not ready to be formalized because some prerequisites (especially "entropy-pfr" Theorem 6.16) do not even have formalized statements yet.
Clicking on the Lean link below the PFR statement in the dependency graph takes you to the corresponding Lean document:

This is what a typical theorem looks like in Lean. There are many assumptions before the colon, such as:
G is a finite elementary abelian group of order 2 (this is how the team chose to formalize finite field vector spaces); A is a nonempty subset of G; the cardinality of A+A is less than K times the cardinality of A.
The statement after the colon is the conclusion: A can be covered in the form of c+H, where c is a set with at most
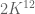
elements, in the subgroup H of G.
Astute readers may notice that the theorem above seems to lack a detail or two, for example, it does not explicitly assert that H is a subgroup.
This is because the "pretty printing" mode suppresses some information in the theorem statement, which can be seen by clicking on the "source" link.

It can be seen that H needs to have the type of a subgroup of G.
There is a prominent "sorry" at the bottom of the theorem, indicating that the proof for the theorem has not been provided yet, but the ultimate intention is, of course, to replace this "sorry" with an actual proof.
Filling in this "sorry" is currently difficult, so a simpler task needs to be found.
Below is a simple intermediate lemma "ruzsa-nonneg" that appears in the proof:
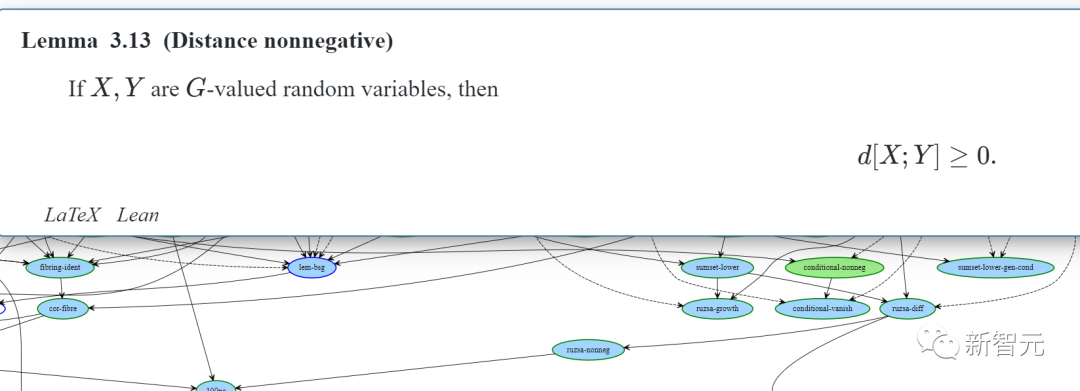
The expression
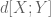
refers to the Ruzsa distance of entropy between X and Y, which is a real number.
The bubble is blue with a green border, indicating that the statement has been formalized, and the proof is ready for formalization.
The Blueprint dependency graph shows that this lemma can be derived from a previous lemma called "ruzsa-diff":
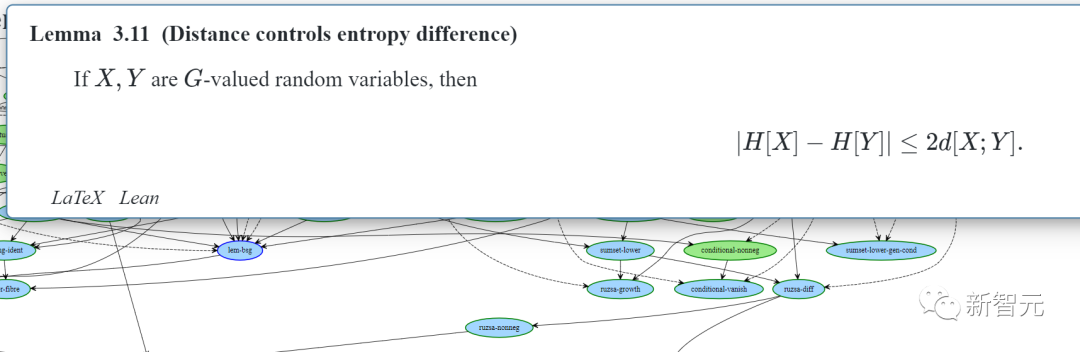
The "ruzsa-diff" is also blue with a green border, so it has the same current status as "ruzsa-nonneg": the statement has been formalized, and the proof is ready for formalization, but the proof has not been written in Lean. Here,
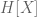
represents the Shannon entropy of X.
By observing Lemma 3.11 and Lemma 3.13, we can clearly see that |H[X] - H[Y]| is obviously non-negative.
Therefore, even though we don't yet know how to prove Lemma 3.11, assuming Lemma 3.11 is true and completing the proof of Lemma 3.13 should be straightforward.
The formalization of Lemma 3.11 is as follows: ("sorry" indicates that the lemma currently has no proof)

Similarly, the formalization of Lemma 3.13 is:

Now, let's try to fill in the second "sorry".
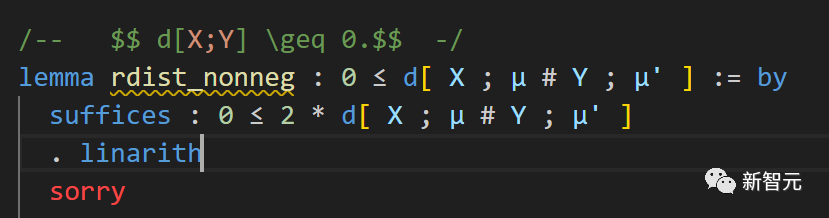
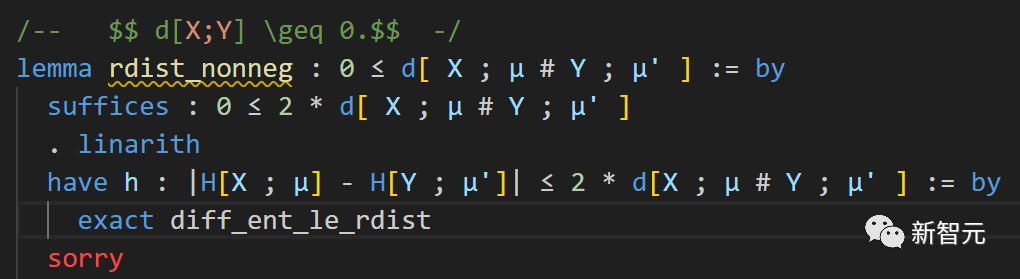
In the local copy of the PFR GitHub repository, Terence Tao opened the relevant Lean file in an editor (Visual Studio Code with the lean4 extension) and navigated to the "sorry" of "rdist_nonneg".
The accompanying "Lean Information View" shows the current status of the Lean proof:
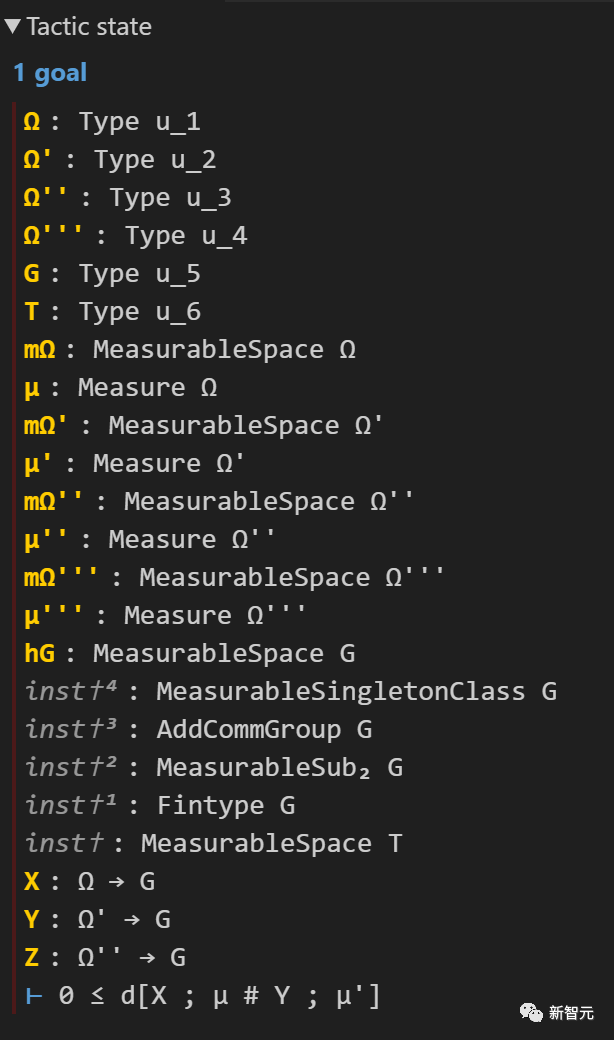
At the bottom, the target we need to prove is visible.
Next, a series of "tactics" will be used to change the target and/or assumptions in proving this statement.
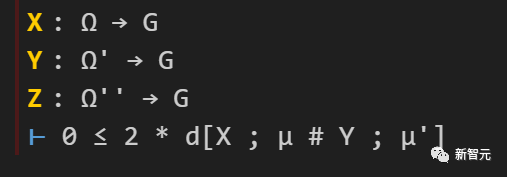
The first step is to introduce the factor 2 required to apply Lemma 3.11.
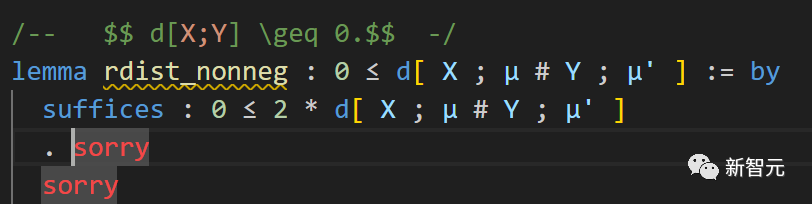
Now, we have two targets (and two "sorry"s): one is to prove
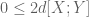
equivalent to
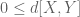
; the other is to prove
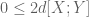
.
The state after filling in the first "sorry" is as follows (some irrelevant assumptions have been removed):
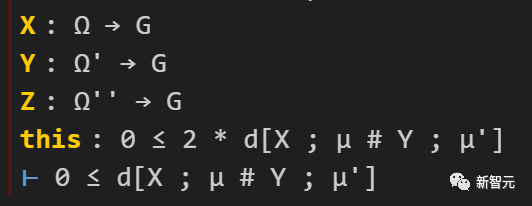
Here, a very convenient "linarith" strategy can be used, which can solve any target derived from linear operations based on existing assumptions:
After successful completion, the status report shows that this branch no longer has any targets to prove. So, we move on to the remaining "sorry", which is to prove
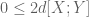
:
Here, we will attempt to reference Lemma 3.11. To do this, Terence Tao added a few lines of code:
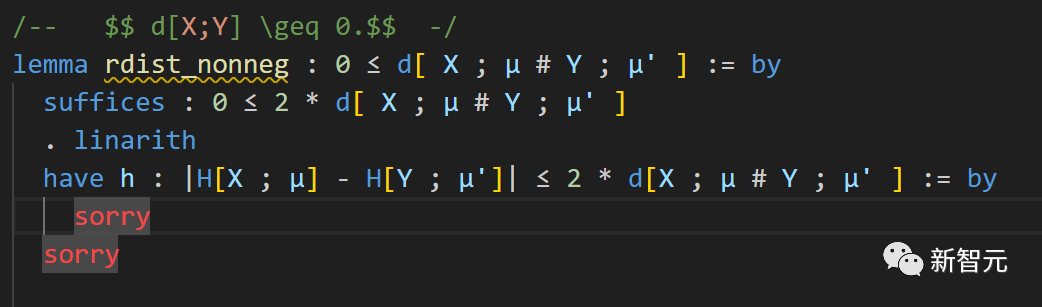
As a result, we now have two sub-targets: one is to prove the constraint
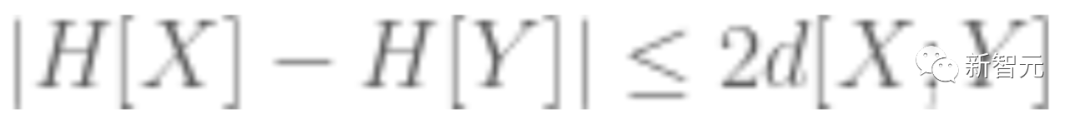
(referred to as "h"), and the other is to derive the previous target from h
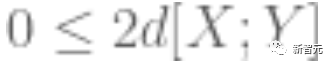
.
For the first target, the "diff_ent_le_rdist" lemma, which is being coded, needs to be invoked.
One way to do this is to try using the "exact?" strategy, which automatically searches to see if the target can be immediately derived from existing lemmas:
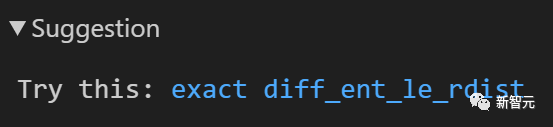
Terence Tao clicked on the suggested code (the system will automatically paste it in the correct place). The result was successful, leaving only the final "sorry":
Here, Terence Tao used the "exact?" strategy and followed its suggestion to establish a matching boundary
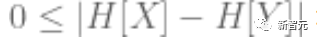
:

In completing the final "sorry", Terence Tao once again tried "exact?" to find out how to combine h and h' to achieve the expected target, and it was successful!

It can be seen that all the underscores have disappeared. In other words, Lean has considered it a valid proof.
By omitting several intermediate steps, we can compress this proof quite tightly:

Now the proof is complete!
What we have finally obtained is basically a "single-line proof", which is reasonable considering how close Lemma 3.11 and Lemma 3.13 are.
Then, Terence Tao pushed all the content back to the main Github repository.
The reconstruction of the Blueprint takes quite a long time (about half an hour), and the dependency graph now shows "ruzsa-nonneg" in green:
Therefore, it can be said that the formalization of PFR is closer to completion.
However, even though "ruzsa-nonneg" is now colored green, there is still no complete evidence for this result, because the lemma it depends on, "ruzsa-diff", is not green.
From this perspective, the proof is still locally completed.
Terence Tao expressed hope that at some point in the future, the precursor result can also be proven, at which point it can be said that the result of the PFR conjecture has been fully proven.
References:
https://news.ycombinator.com/item?id=38528582
https://terrytao.wordpress.com/2023/11/18/formalizing-the-proof-of-pfr-in-lean4-using-blueprint-a-short-tour/
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




