In this article, we will introduce a new type of automated market maker (AMM) specifically designed for prediction markets: pm-AMM.

Written by: Ciamac Moallemi, Dan Robinson, Paradigm

Translated by: Yangz, Techub News

Introduction

In this article, we will introduce a new type of automated market maker (AMM) specifically designed for prediction markets: pm-AMM.

AMMs and their predecessors (such as market scoring rules) were originally invented as a way to provide liquidity for prediction markets. Now, they dominate the trading volume of most DEXs. However, ironically, despite the sharp increase in trading volume in prediction markets, most of it uses order books rather than AMMs.

One possible reason is that existing AMMs are not suitable for outcome tokens (i.e., if the event occurs, the token's price is $1, and if the event does not occur, the token's price is $0). The volatility of outcome tokens depends on the current probability of the event and the time until the prediction market expires, meaning that the liquidity provided by the asset pool is inconsistent. Once the prediction market expires, liquidity providers (LPs) essentially lose all their value.

To address this, we propose a new type of AMM optimized around these considerations, aimed at solving a long-standing question in AMM research: what does it mean to optimize an AMM for specific types of assets? In other words, how would a model for a certain asset (such as options, bonds, stablecoins, or outcome tokens) affect the AMM we apply? We propose a possible answer to this question based on the concept of Loss vs. Rebalancing (LVR).

Research Findings

We established a model for the price movements of some outcome tokens, which we call the Gaussian score dynamics model. This model may be applicable to prediction markets and can predict whether certain fundamental random trends (such as the score difference in a basketball game, the vote difference in an election, or the price of certain assets) will exceed a certain value at a specific expiration time in the future.

Using this model, we derived a new invariant-based AMM for these tokens, namely the static pm-AMM invariant:

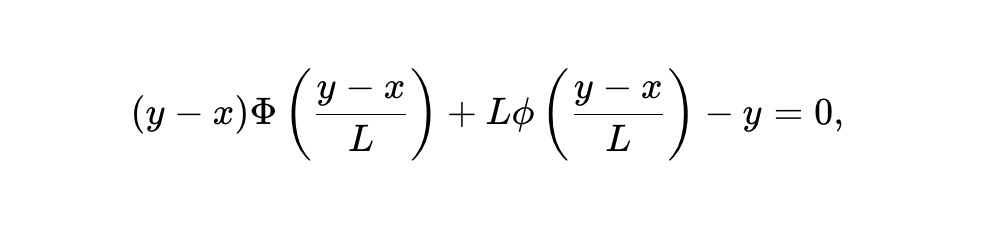
Where x is the reserve of outcome tokens in the AMM, y is the reserve of its opposing, complementary outcome tokens, L is the overall liquidity or proportionality coefficient, and ϕ and Φ represent the probability density function and cumulative distribution function of the normal distribution, respectively.

The above invariant is based on a powerful concept, Loss vs. Rebalancing (LVR), which we can view as the rate at which the AMM incurs losses due to arbitrage, with LVR depending on the shape of the AMM and the price movements of the relevant assets traded on the AMM.

We define a uniform AMM for a certain asset as one where, if used for that asset, the LVR of the AMM is proportional to its portfolio value at any given moment, regardless of the current price. Milionis et al. argue that for assets whose prices follow geometric Brownian motion (GBM, a popular model for the price movements of ordinary assets like stocks and cryptocurrencies), constant geometric mean market makers (such as Uniswap and Balancer) are the only uniform AMMs, while the static pm-AMM is the uniform AMM for asset behaviors that follow our proposed Gaussian score dynamics model for outcome tokens.

While the static pm-AMM has a uniform LVR (as part of the portfolio value) at all prices, the LVR will still increase as the expiration date of the prediction market approaches. This is because prediction markets can be very volatile as they near expiration. To adjust the pm-AMM to reduce its liquidity, thereby keeping the expected LVR at all moments during the remaining time before expiration constant, we derived the dynamic pm-AMM invariant, which depends on the time to expiration T-t:

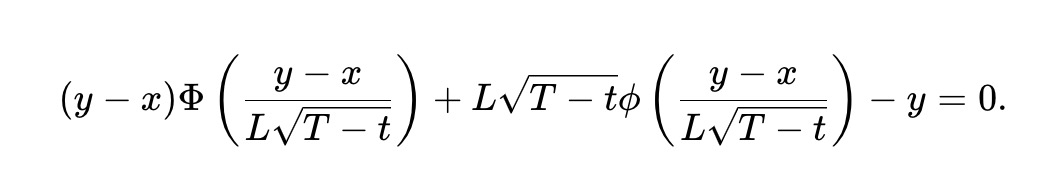
The mechanism of the dynamic pm-AMM prevents the LVR from increasing as the expiration date approaches by providing continuously decreasing liquidity. In real liquidity pools, this may not be desirable, especially since non-arbitrage trading activity (and the fees generated from it) may also increase over time. However, the pm-AMM provides a framework for liquidity providers to adjust liquidity based on expected fees and how they wish to allocate arbitrage risk.

These AMMs may help guide passive liquidity in on-chain prediction markets. The concept of uniform AMMs and related methods may also be broadly applicable to DEX designers, who can use these methods to customize AMMs for other types of assets whose price movements do not follow geometric Brownian motion, such as stablecoins, bonds, options, or other derivatives.

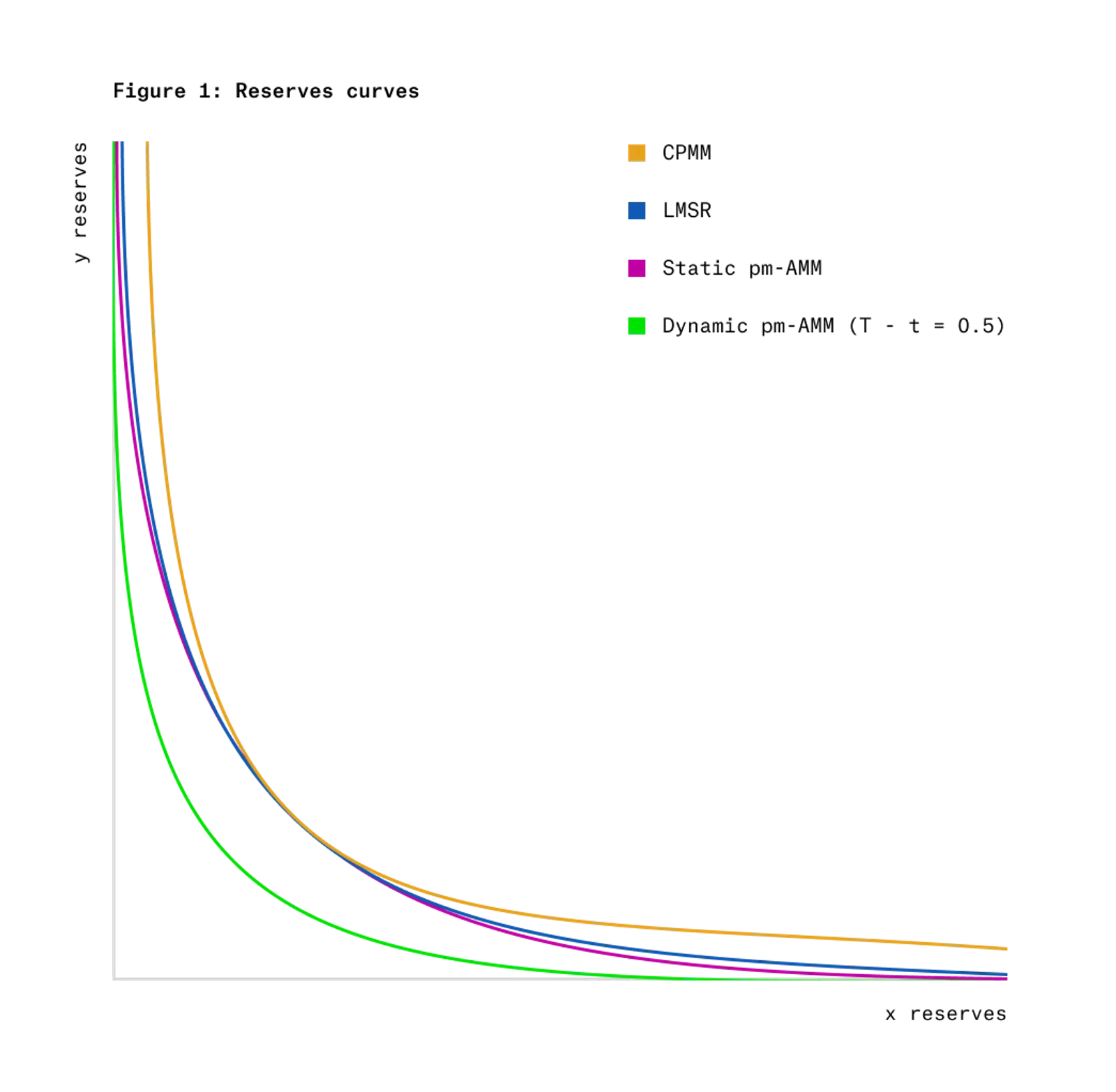
Figure 1 shows the invariant curves of static and dynamic pm-AMMs, compared with other well-known invariant curves, namely constant product market makers (CPMM) and logarithmic market scoring rules (LMSR). Note that the reserve curve of the dynamic pm-AMM provides lower liquidity over time.

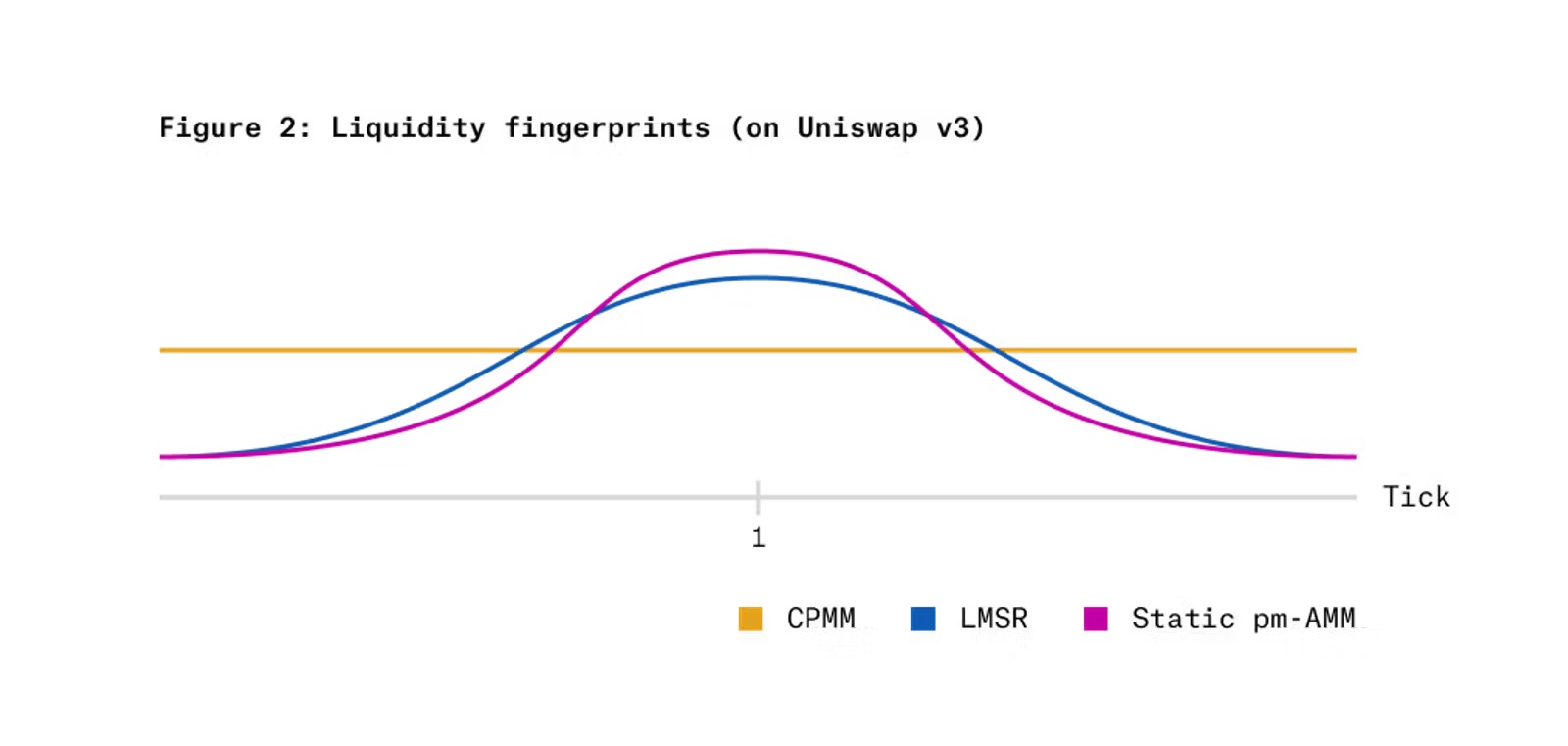
Figure 2 shows the "liquidity fingerprint" that would occur if the static pm-AMM invariant were implemented on Uniswap v3 concentrated liquidity AMM, compared to CPMM and LMSR. The horizontal axis corresponds to the logarithmic scale of relative prices (the price of x tokens divided by the price of y tokens), and the vertical axis corresponds to the liquidity of each AMM at that price level. It can be seen that, compared to these two alternatives, the pm-AMM concentrates more liquidity at a relative price of 1 (probability of 50%, i.e., the token price equals 0.50), while concentrating less liquidity at extreme relative prices (very low or very high).

Research Background

Prediction Markets

Prediction markets are an increasingly popular application in cryptocurrency. As of October 2024, Polymarket's trading volume has exceeded $2 billion. However, most of the liquidity in cryptocurrency prediction markets is provided on order books rather than AMMs, despite the latter dominating the trading volume of most cryptocurrencies on DEXs.

One possible reason is that the price behavior of outcome tokens differs from that of ordinary assets, making AMMs designed for them unable to operate stably. For example, imagine a prediction market about a coin toss game, where someone will toss a coin 1001 times, and each outcome (heads or tails) corresponds to two tokens, x and y. Ultimately, if heads outnumber tails, the value of the x token is $1, and if tails outnumber heads, the value of the x token is $0; the y token is the opposite.

The volatility of these outcome tokens largely depends on the remaining tosses and the current toss situation. The closer the current situation is, and the fewer remaining tosses there are, the greater the volatility of these tokens. This means that the losses of constant product market makers (which depend on volatility, as discussed below) vary significantly over time.

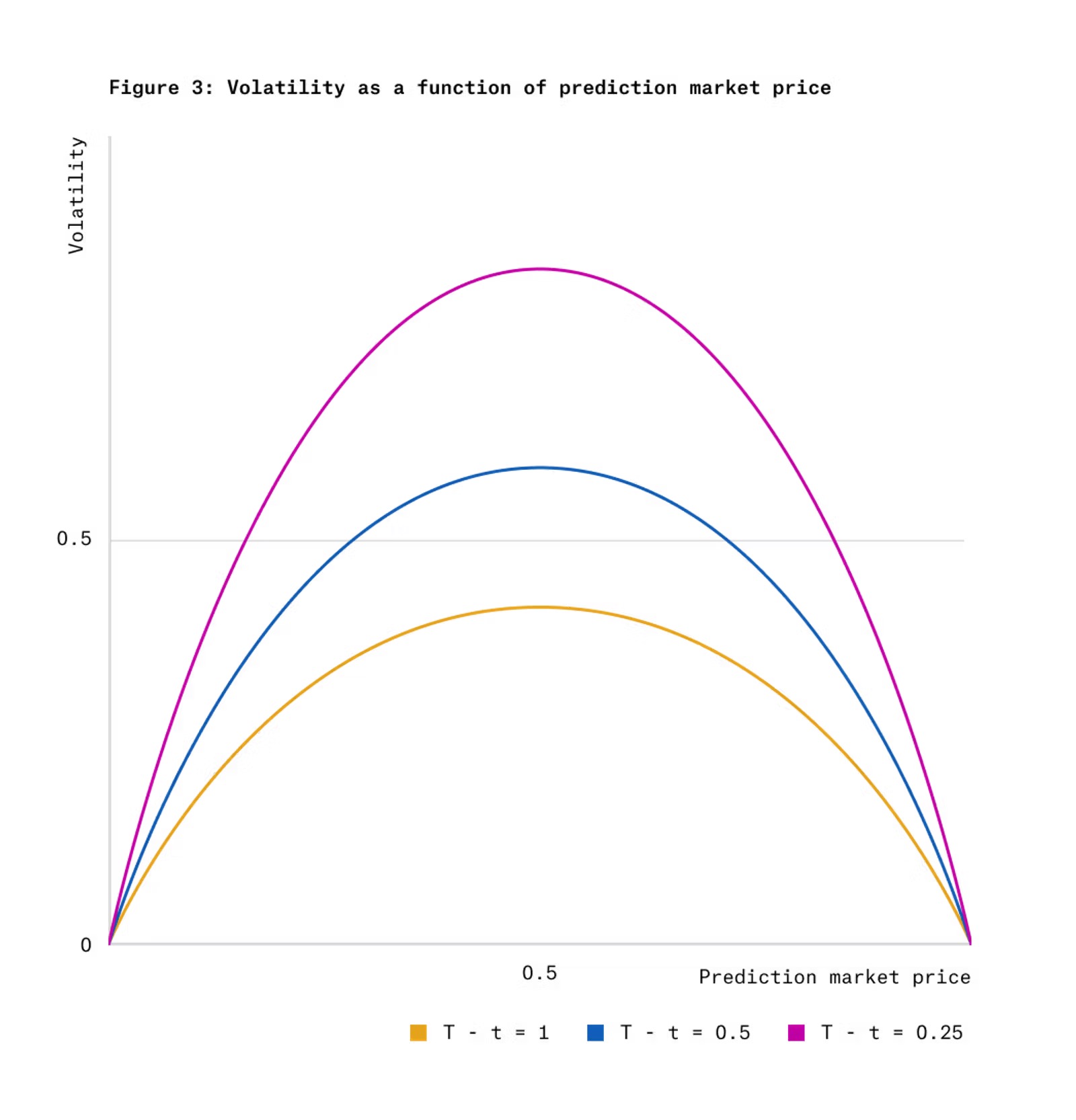
Figure 3 shows the relationship between the volatility of outcome token prices and the function of token prices and remaining time under Gaussian score dynamics conditions.

Many popular prediction markets are actually similar to this coin toss example, betting on whether a certain random trend will end above or below 0 at a future expiration time. For example:

• In a prediction market about the outcome of a basketball game, the market expires once the remaining time in the game is 0. The random trend is the score difference between the two teams.
• A prediction market about the outcome of a presidential election expires on election day. The random trend is the difference in the number of voters intending to vote for each candidate.
• In a prediction market about whether the price of an asset like Bitcoin will be above a certain strike price on a future date, the random trend could be the logarithm of the current Bitcoin price minus a certain strike price.

The price movement model of outcome tokens defined in this article, namely the Gaussian score dynamics model, is inspired by such examples. This model assumes that the prices in prediction markets match the probabilities of certain potential Brownian motions ending above 0. This model is similar to the Black-Scholes model for binary options (binary options are a tool that pays a fixed dollar amount if the asset price is above a certain strike price; if the asset price is below a certain strike price, it pays $0). However, in our model, there is no requirement for the underlying process to correspond to the price of a tradable asset.

We do make a simplifying assumption that the price of the outcome token matches the probability that it is worth $1. This assumption overlooks important market features, including risk and time preference, so studying how these features affect this model will be a topic for future research.

Additionally, we should note that not all prediction markets are suitable for the Gaussian score dynamics model, as this model assumes that the speed at which new information appears is predictable. For example, basketball games may be more suitable for this model than soccer games, as the scoring frequency in basketball is much higher, making the evolution of score differences more consistent over time. Furthermore, some types of prediction markets are entirely different from this model, such as predicting whether a certain one-time unexpected event (like an earthquake) will occur before a specific date. However, this model may serve as a useful starting point for other dynamic derivation models and can demonstrate a method for deriving uniform AMMs for any model.

Loss vs. Rebalancing and Uniformity

After clarifying this model, we derived a mechanism that may be more suitable for these tokens than existing AMMs (such as constant product market makers or LMSR). The guiding metric we used is the expected loss rate for liquidity providers, which can be characterized as "Loss vs. Rebalancing" (LVR).

LVR captures the main adverse selection cost of AMMs: in the absence of trading, the prices of AMMs are static, while as new information emerges, prices become outdated. LVR reflects the costs incurred by AMM liquidity providers, as these outdated prices are exploited by more informed arbitrageurs who will engage in arbitrage trading at prices unfavorable to the AMM. Therefore, LVR can be viewed as the fees that AMMs pay to arbitrageurs to correct their prices.

In addition, in the absence of trading fees, LVR is also the loss incurred by liquidity providers when delta hedging their LP positions by holding the same number of short positions as the tokens that are part of the pool reserves. Therefore, LVR is built upon the main insights of the Black-Scholes option pricing model. Just as options eliminate market risk through delta hedging with the underlying asset, LVR values the LP positions in the AMM after eliminating market risk. In other words, LVR isolates the specificity of being a liquidity provider in the AMM rather than simply bearing the market risk of holding tokens equal to the AMM reserves.

We consider a simple invariant-based AMM without fees or MEV recovery mechanisms. In this case, the AMM will inevitably incur losses due to arbitrage, and no AMM invariant can eliminate LVR (except for invariants that fundamentally do not generate trades). Furthermore, even "minimizing" LVR has no practical significance, as reducing LVR merely means reducing the liquidity provided.

However, while we cannot eliminate LVR, we can make LVR more uniform, so that the percentage of the asset pool value lost does not depend on the current price of the asset. We refer to this property as uniformity.

Imagine a sponsor willing to provide liquidity in a zero-fee prediction market to understand the market's predictions about outcomes. The sponsor will incur losses, but they would prefer to spread the losses evenly rather than concentrating them at specific times or prices. In this case, the current portfolio value of the asset pool can be viewed as the sponsor's "budget." In a uniform AMM, if the sponsor injects $1 of liquidity at a certain time, their expected loss at the next time point is independent of the current state of the fund pool.

Moreover, uniformity also has potential implications for profit-seeking liquidity providers. Even if the AMM can derive some profit from loss vs. rebalancing, or even turn a profit (through non-zero swap fees or auction mechanisms like MEV tax), it still requires some strategy to determine how to allocate liquidity at different prices and times. We can view the expected loss of a zero-fee pool as a way to measure how much liquidity to allocate at a specific time, taking into account the price process of the asset.

We define a uniform AMM for a specific asset as one where, regardless of the current price of the asset, its expected LVR is a constant fraction of the current value of the asset pool. Note that whether an AMM has a uniform LVR depends on the price process of the asset itself. As shown in Appendix B.2 by Milionis et al., if the price of the asset follows geometric Brownian motion, then the essentially unique uniform AMM between the asset and the warehouse is the weighted geometric mean market maker, whose invariant is:

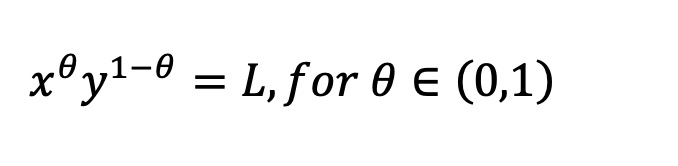
This is the formula used in Balancer, and the constant product market maker used in Uniswap v2 is also a special case of this. However, for tokens that follow Gaussian score dynamics, the constant geometric mean AMM does not have a uniform LVR. The logarithmic market scoring rule (LMSR) is the same.

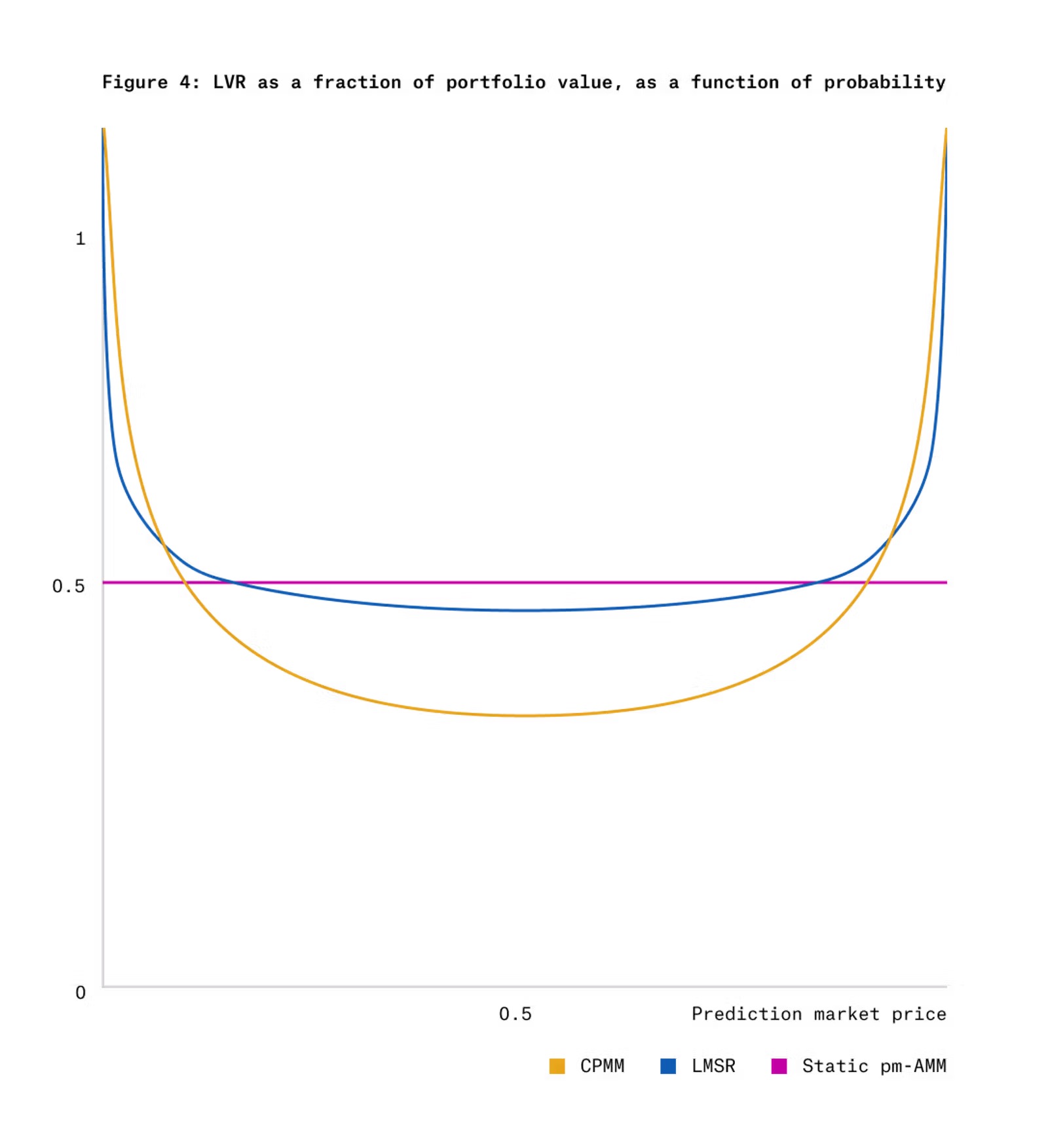
Figure 4 shows the LVR for Gaussian score dynamic outcome tokens at time T-t=1, comparing CPMM and LMSR with the uniform LVR of static pm-AMM.

For these reasons, we developed two AMMs designed for prediction markets under Gaussian score dynamics: one has a uniform LVR at any given time, but the LVR increases as the expiration date of the prediction market approaches; the other has a uniform LVR and constant expected LVR over the remaining time range.

As seen in Figure 4, when the price of the outcome token is at extreme values close to zero or one, CPMM and LMSR exhibit larger LVRs. This is because, although the price volatility near these points is low (see Figure 3), the decay rate of the asset pool value is faster at extreme prices. Therefore, a uniform AMM should provide less liquidity at extreme prices, which is precisely what the pm-AMM design accomplishes (see Figure 2).

Previous Research

AMMs originated from prediction markets and market scoring rules (such as LMSR). These rules led to the discovery of constant function market makers (CFMM), such as Uniswap v2, which are characterized by an invariant relationship between the reserves of each asset. AMMs based on this design have become the mainstream market mechanism for DEXs in recent years.

Recently, financial economics perspectives have been applied to understand the costs of automated market makers, taking the form of loss vs. rebalancing (LVR), primarily focusing on geometric Brownian motion. On the other hand, the price dynamics of prediction markets are very different, as they have limited returns and finite time horizons. Taleb proposed dynamics based on observable voting processes, while we developed another dynamic based on observable Gaussian score processes.

There have been some applied studies on designing automated market makers for non-GBM assets. One example is StableSwap, an AMM designed for stablecoin pairs, which is based on an intuitive premise that the automated market maker between related assets and mean-reverting assets should concentrate liquidity tightly at one price, but its derivation does not involve modeling the asset price process. Another example is YieldSpace, an AMM designed specifically for zero-coupon bonds. While the derivation of YieldSpace does involve a simple zero-coupon bond pricing model, it does not include a complete price process model (without modeling the evolution of interest rates).

Additionally, there has been some academic work focused on designing real-time market models around beliefs about asset price behavior. One example is the design by Goyal et al. Their framework is designed to maximize expected active liquidity rather than to make expected losses uniform, which sometimes leads to results contrary to ours. For instance, their derivation suggests that if liquidity providers expect the relative price of the asset to remain around 1, then LMSR (which concentrates liquidity near price 1 compared to CPMM) is very suitable; whereas our framework suggests that if expected prices are expected to diverge (as with outcome tokens), there is reason to concentrate liquidity near 1.

Various AMM Models

Automated Market Makers

We can consider a prediction market concerning a single event and an AMM trading two competing assets. One risk asset is represented by x, which pays $1 if the event occurs, and pays nothing otherwise; the other risk asset is represented by y, with the opposite payment structure. The AMM maintains the invariant f(x,y)=L, where f(⋅,⋅) is the invariant function of the reserves (x,y), and L is a constant. Given the price P (in dollars) of the x asset, the value function of the asset pool is:

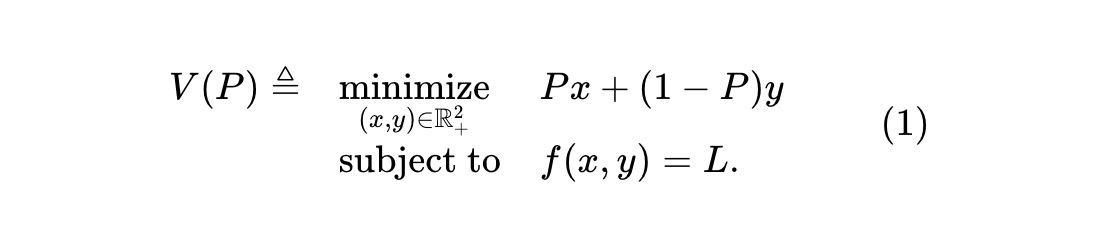
This is the value of the asset pool when the price of x is P. Since holding one unit of both x and y assets is equivalent to holding cash, we must set the price of y to 1-P. Assume there is a group of arbitrageurs who can observe the price Pt of the x asset (and the price 1-Pt of the y asset) at each time t. Assuming no trading fees or other frictions, these arbitrageurs will continuously monitor the AMM and attempt to extract value from any mispricing by the AMM. In pursuit of their own profit maximization, they will trade against the AMM to minimize the value of the AMM reserves. If we denote the reserve value at time t (when the price is Pt) as Vt, then Vt = V(Pt).

Example 1: In the case of a constant product market maker (CPMM), the invariant is f(x,y)≜xy, and the value function of the asset pool is:

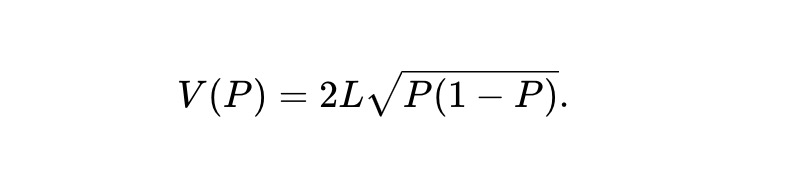
Example 2: The logarithmic market scoring rule (LMSR) created by Robin Hanson can be viewed as an AMM that satisfies the following invariant.

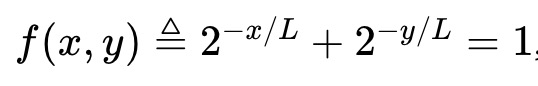
Its asset pool value function is (proportional to the binary entropy of the event implied by the price):

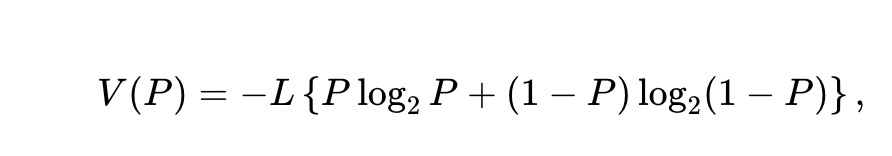
Let x∗(P) and y∗(P) denote the optimal solutions to optimization problem (1), assuming they exist, are unique, and are sufficiently smooth functions of price P, then the following formula is similar to Theorem 1 by Milionis et al., but applicable to the current environment:

Theorem 1. For all prices P≥0, the value function of the asset pool satisfies:

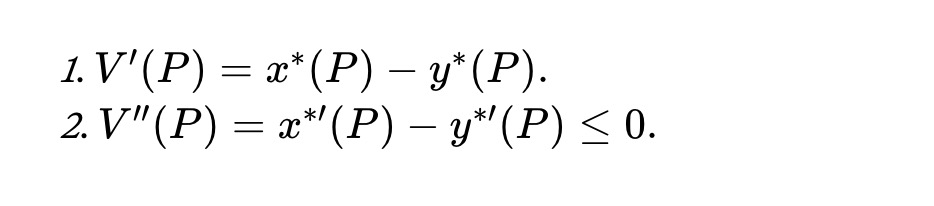
Gaussian Score Dynamics

How do the prices of risk assets evolve over time according to what we call Gaussian score dynamics? Specifically, we assume there exists a stochastic process {Zt} over the time interval t∈[0,T], where the event is determined by the sign of Zt at the end of the time span t=T: if ZT≥0, then the x asset pays off; if ZT<0, then the y asset pays off. We can understand Zt as the score difference between two teams in a bilateral competition. Thus, we will view Zt as the scoring process. Note that while our model assumes the existence of this scoring process, the AMM does not need to directly observe these processes. As described below, the AMM can infer the current value of the score based on the marginal price (after arbitrage) and the time to expiration.

We assume Zt follows a random walk. Specifically, we assume Zt is a Brownian motion with volatility σ>0, i.e., dZt=σdBt, where Bt is standard Brownian motion. Then, it is not difficult to see that the price Pt of the x asset at time t is:

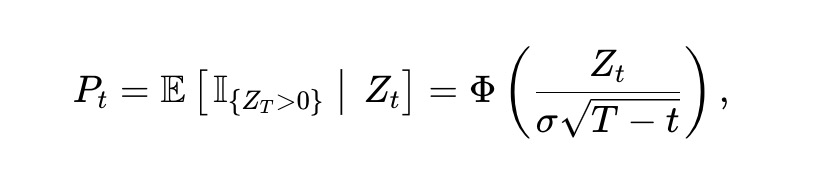
Where, Φ(⋅) is the standard normal cumulative distribution function (CDF). By applying Itô's theorem, Pt must satisfy:

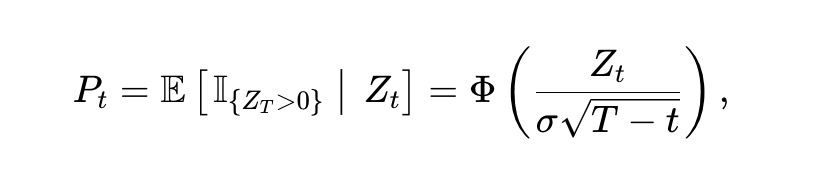
Where, ϕ(⋅) is the standard normal probability density function, and Φ-1(⋅) is the inverse CDF. Note that while the score dynamics and the conversion or reverse conversion of scores to prices depend on σ, the dynamics of the isolated price process Pt do not depend on σ. The volatility of these dynamics in relation to price and remaining time is shown in Figure 3.

Uniform AMM

According to the discussion above, if we denote Vt as the value of the asset pool reserves at time t (when the price is Pt), then Vt=V(Pt). By applying Itô's theorem, we can derive that the value of the asset pool changes according to the following formula:

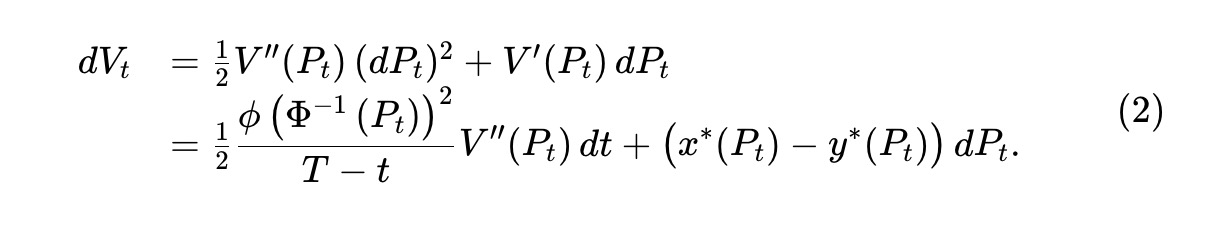
Since the price Pt is a martingale, the second term of (2) is also a martingale, which may be increasing or decreasing. However, according to V(⋅) (see Theorem 1), the first term corresponds to a negative transformation, thus it is a decreasing process. This captures the value lost by arbitrageurs who hedge against the asset pool at unfavorable prices, as proposed by Milionis et al. We define the instantaneous rate of this loss as:

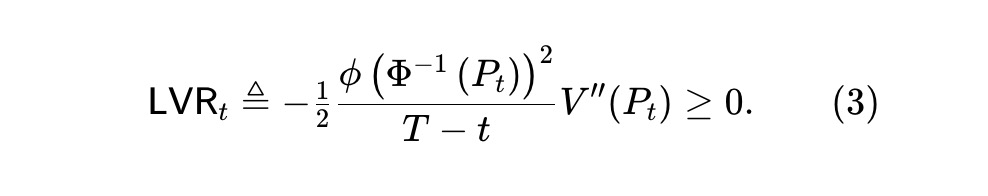
Milionis et al. found that for assets following geometric Brownian motion, essentially only the geometric mean market maker is a uniform AMM. In the prediction market under Gaussian score dynamics, to examine (3), the uniform LVR pool must solve the following ordinary differential equation (ODE):

This is impossible because the left side of the equation depends on t, while the right side does not. The core issue here is that the dynamics of geometric Brownian motion are invariant across time, while Gaussian score dynamics are highly time-dependent.

To circumvent this issue, we allow α to be time-dependent, meaning we can set α=β/(T-t), where β>0, and consider a setup such that:

This is equivalent to the ODE for P≥0. Additionally, V(⋅) has some extra requirements, such as V′′(P)≤0 (refer to Theorem 1).

Static pm-AMM

The above ODE can be simplified by changing the variable u=Φ-1(P). When β=1/2, there exists a solution that satisfies both the ODE and the additional concavity requirement, which is:

The reserves of tokens x and y are:

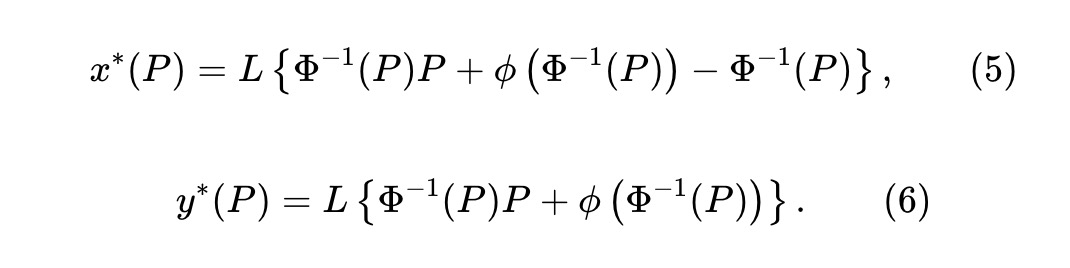
Here, L≥0 is a liquidity parameter that determines the scaling of the fund pool size. Observing y∗(P)-x∗(P)=LΦ-1(P), and substituting it into (5), the reserves (x,y) of the fund pool must satisfy the invariant:

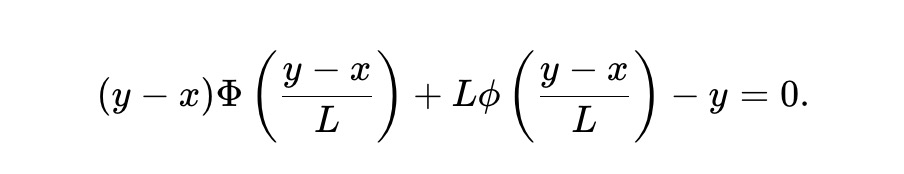
This defines the static pm-AMM. By design, this AMM satisfies the following relationship:

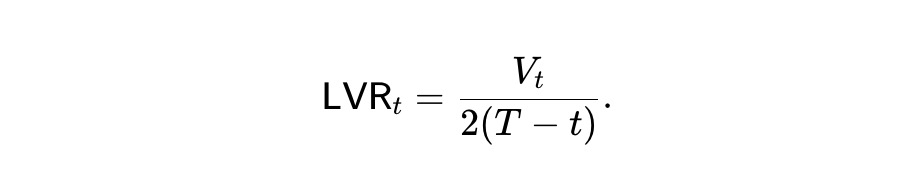
Defining Vˉt=E[Vt] as the expected pool value, we can derive from (2):

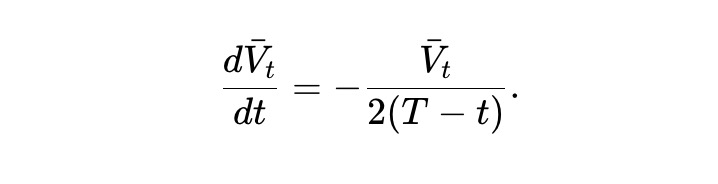
Solving this ordinary differential equation yields the following result. In other words, under expected conditions, the asset pool value of the static pm-AMM decays according to the square root of the remaining time range.

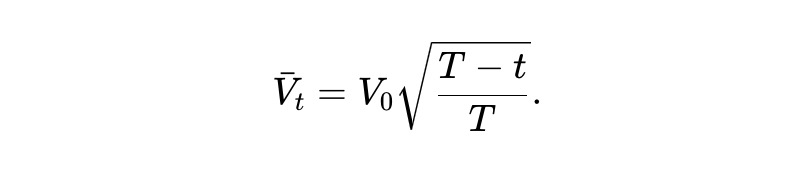
Dynamic pm-AMM

One drawback of the static pm-AMM is that while its LVR per dollar value is uniform across all possible prices, it changes over time. Specifically, the loss per dollar value is inversely proportional to the time to expiration, thus it will increase over time until it loses all value at expiration.

Dynamic liquidity. We envision a dynamic variant of the static pm-AMM design, where AMM LPs withdraw liquidity over time to reduce losses. Specifically, assume the value of the fund pool is:

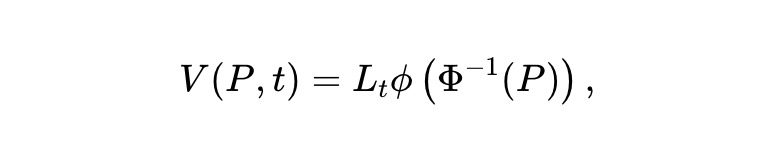
Where Lt is a deterministic smooth function that determines the extent to which liquidity is removed (or possibly added) over time. Applying Itô's theorem to the asset pool value process Vt≜V(Pt,t), we have:

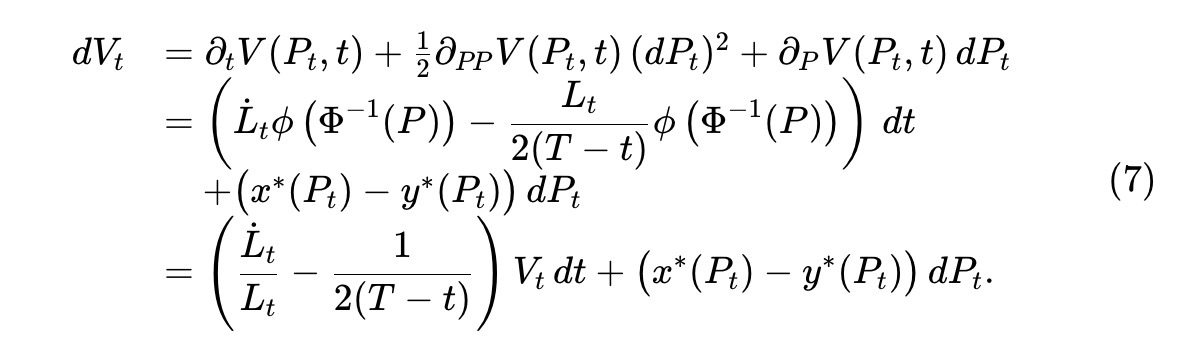
Let Ct denote the cumulative dollar value of withdrawn liquidity. Since the value of the fund pool is linearly related to the liquidity Lt, the dollar value of changes in Lt is proportional to Vt/LT. We can obtain:

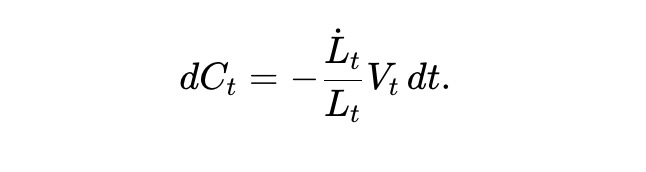
The total wealth Wt of AMM LPs consists of the value of the fund pool reserves and the accumulated value of withdrawn liquidity, thus Wt=Vt+Ct, and satisfies:

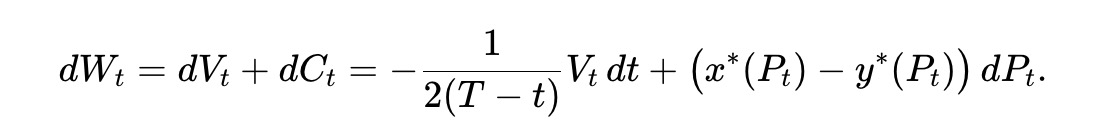
This means that the expected wealth of LPs Wˉt≜E[Wt] satisfies the following condition, where Vˉt≜E[VT］.

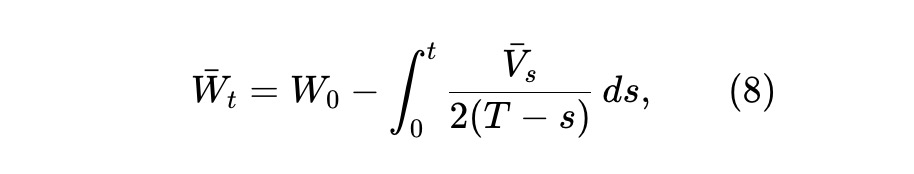
Now, consider the specific choice of the liquidity curve as follows:

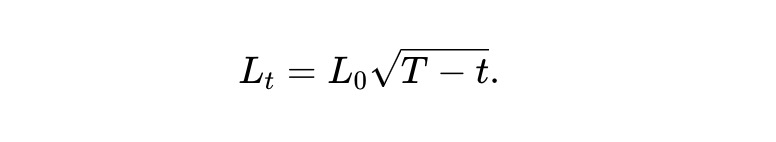
We call this the dynamic pm-AMM. According to (7), the expected asset pool value Vˉt=E[Vt] satisfies:

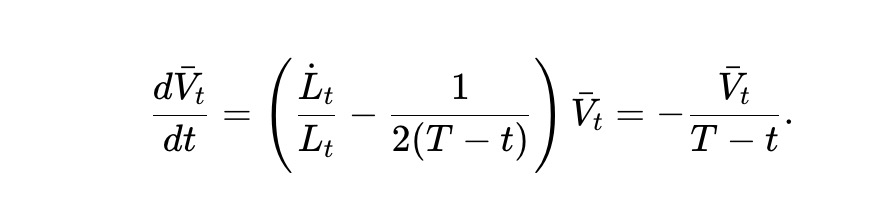
Solving this ordinary differential equation yields the following result.

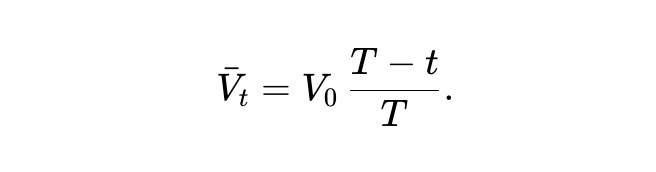
In other words, in the dynamic pm-AMM, after deducting withdrawals, the expected value of the fund pool decreases linearly. Furthermore, since it inherits the value function of the static pm-AMM, the LVR loss rate per unit time is:

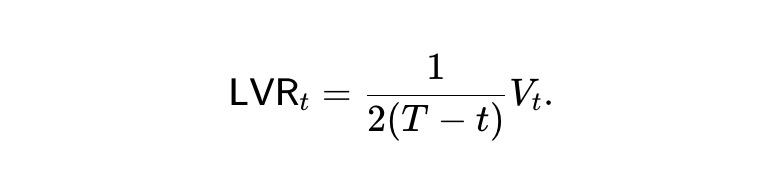
The expected loss rate is as follows, remaining constant during the period t. In other words, over time, the dynamic pm-AMM will lose the funds of arbitrageurs at a constant rate (on average).

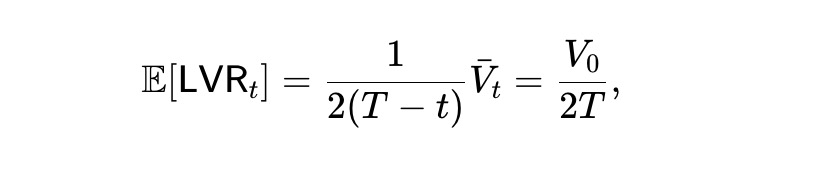
Finally, according to (8), the expected wealth process is illustrated in the following figure. Thus, half of the initial wealth will be lost in the end.

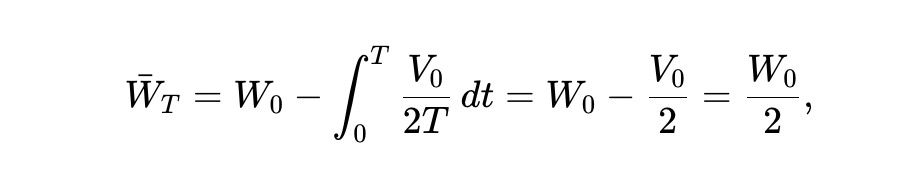
Conclusion

The pm-AMM may be suitable for prediction markets driven by dynamics such as Gaussian score dynamics models. In addition, our research suggests that uniform AMMs may be applicable to other types of assets, such as bonds, options, and other derivatives.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。