Author: mutourend & lynndell, Bitlayer Labs
Original Title: "Binius STARKs Analysis and Its Optimization"
Original Link: https://blog.bitlayer.org/Binius_STARKs_Analysis_and_Its_Optimization/
Abstract: The bit widths of the 1st, 2nd, and 3rd generation STARK proof systems are 252, 64, and 32 bits respectively. Although encoding efficiency has improved, there is still wasted space. Binius directly operates on bits, providing compact and efficient encoding, and is likely to be the future 4th generation STARK. Binius employs techniques such as tower-based binary field arithmetic, an improved version of HyperPlonk product and permutation checks, and small field polynomial commitments to enhance efficiency from various angles. Further optimizations can be made in binary field multiplication, ZeroCheck, SumCheck, PCS, etc., to further improve proof speed and reduce proof size.
1 Introduction
Unlike elliptic curve-based SNARKs, STARKs can be viewed as hash-based SNARKs. A major reason for the current inefficiency of STARKs is that most numerical values in actual programs are small, such as indices in for loops, boolean values, counters, etc. However, to ensure the security of Merkle tree-based proofs, using Reed-Solomon encoding to expand data results in many additional redundant values occupying the entire field, even when the original values themselves are very small. To address this issue, reducing the size of the field has become a key strategy.
As shown in Table 1, the encoding bit widths of the 1st generation STARKs is 252 bits, the 2nd generation STARKs is 64 bits, and the 3rd generation STARKs is 32 bits, but the 32-bit encoding width still has a lot of wasted space. In contrast, the binary field allows direct bit operations, providing compact and efficient encoding without arbitrary wasted space, which is the 4th generation STARK. 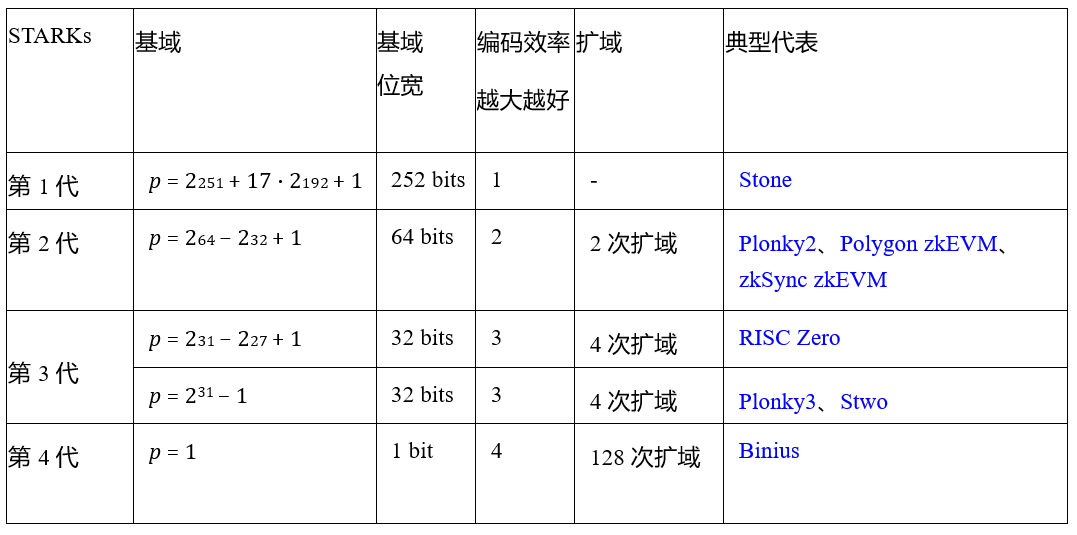
Table 1: Evolution Path of STARKs
Compared to finite fields discovered in recent years such as Goldilocks, BabyBear, and Mersenne31, research on binary fields can be traced back to the 1980s. Currently, binary fields are widely used in cryptography, with typical examples including:
- Advanced Encryption Standard (AES), based on the F28 field;
- Galois Message Authentication Code (GMAC), based on the F2128 field;
- QR codes, using Reed-Solomon encoding based on F28;
- Original FRI and zk-STARK protocols, as well as the Grøstl hash function, which entered the SHA-3 finals and is based on the F28 field, making it a very suitable recursive hash algorithm.
When using smaller fields, the expansion operation becomes increasingly important for ensuring security. The binary field used by Binius must fully rely on field expansion to guarantee its security and practical usability. Most polynomials involved in Prover computations do not need to enter the expanded field and can operate under the base field, achieving high efficiency in the small field. However, random point checks and FRI calculations still need to delve into a larger expanded field to ensure the required security.
When constructing proof systems based on binary fields, there are two practical issues: the size of the field used to represent the trace in STARKs should be greater than the degree of the polynomial; and when committing to a Merkle tree in STARKs, Reed-Solomon encoding must be performed, and the size of the field used should be greater than the size after encoding expansion.
Binius proposes an innovative solution to address these two issues by representing the same data in two different ways: first, using multivariable (specifically multilinear) polynomials instead of univariate polynomials to represent the entire computation trace through its values on "hypercubes"; second, since each dimension of the hypercube has a length of 2, standard Reed-Solomon expansion cannot be performed as in STARKs, but the hypercube can be viewed as a square, and Reed-Solomon expansion can be performed based on that square. This method greatly enhances encoding efficiency and computational performance while ensuring security.
2 Principle Analysis
The construction of most current SNARK systems typically includes the following two parts:
Information-Theoretic Polynomial Interactive Oracle Proof (PIOP): PIOP serves as the core of the proof system, transforming the input computational relationships into verifiable polynomial equalities. Different PIOP protocols allow the prover to gradually send polynomials through interaction with the verifier, enabling the verifier to validate the correctness of the computation by querying a small number of polynomial evaluation results. Existing PIOP protocols include PLONK PIOP, Spartan PIOP, and HyperPlonk PIOP, each handling polynomial expressions differently, thus affecting the performance and efficiency of the entire SNARK system.
Polynomial Commitment Scheme (PCS): The polynomial commitment scheme is used to prove whether the polynomial equalities generated by PIOP hold. PCS is a cryptographic tool that allows the prover to commit to a polynomial and later verify the evaluation results of that polynomial while hiding other information about the polynomial. Common polynomial commitment schemes include KZG, Bulletproofs, FRI (Fast Reed-Solomon IOPP), and Brakedown. Different PCS have varying performance, security, and applicable scenarios.
Depending on specific needs, different PIOP and PCS can be selected and combined with suitable finite fields or elliptic curves to construct proof systems with different attributes. For example:
• Halo2: Combines PLONK PIOP with Bulletproofs PCS and is based on the Pasta curve. Halo2 focuses on scalability and removes the trusted setup in the ZCash protocol.
• Plonky2: Combines PLONK PIOP with FRI PCS and is based on the Goldilocks field. Plonky2 aims to achieve efficient recursion. When designing these systems, the selected PIOP and PCS must match the finite field or elliptic curve used to ensure the correctness, performance, and security of the system. The choice of these combinations not only affects the proof size and verification efficiency of SNARKs but also determines whether the system can achieve transparency without a trusted setup and whether it can support extended features such as recursive proofs or aggregated proofs.
Binius: HyperPlonk PIOP + Brakedown PCS + binary field. Specifically, Binius includes five key technologies to achieve its efficiency and security. First, the arithmetic based on tower-based binary fields forms the foundation of its computation, enabling simplified operations within the binary field. Second, Binius adapts HyperPlonk product and permutation checks in its interactive Oracle proof protocol (PIOP), ensuring secure and efficient consistency checks between variables and their permutations. Third, the protocol introduces a new multilinear shift proof, optimizing the efficiency of verifying multilinear relationships in small fields. Fourth, Binius employs an improved Lasso lookup proof, providing flexibility and strong security for the lookup mechanism. Finally, the protocol uses a small field polynomial commitment scheme (Small-Field PCS), enabling it to implement an efficient proof system in the binary field and reducing the overhead typically associated with large fields.
2.1 Finite Fields: Arithmetic Based on Towers of Binary Fields
Tower-based binary fields are key to achieving fast verifiable computation, primarily due to two aspects: efficient computation and efficient arithmetic. Binary fields inherently support highly efficient arithmetic operations, making them an ideal choice for performance-sensitive cryptographic applications. Additionally, the structure of binary fields supports a simplified arithmetic process, meaning that operations performed in the binary field can be represented in a compact and easily verifiable algebraic form. These features, combined with the ability to fully leverage their hierarchical characteristics through tower structures, make binary fields particularly suitable for scalable proof systems like Binius! 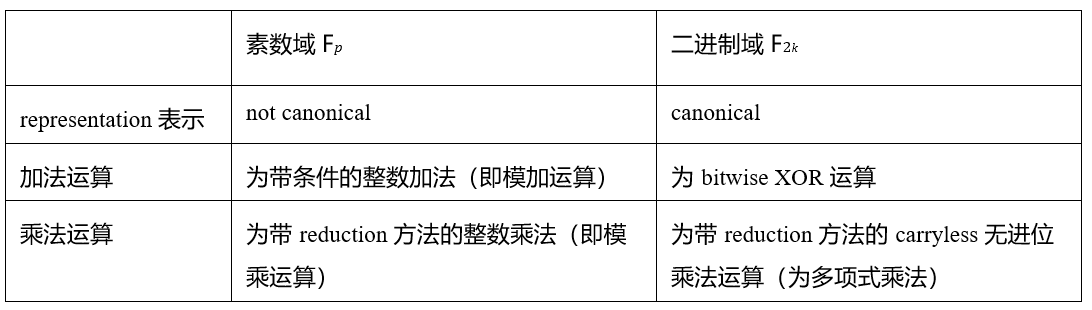
Here, "canonical" refers to the unique and direct representation of elements in the binary field. For example, in the most basic binary field F2, any k-bit string can be directly mapped to a k-bit binary field element. This is different from prime fields, which cannot provide such a canonical representation within a given bit length. Although a 32-bit prime field can be contained within 32 bits, not every 32-bit string can uniquely correspond to a field element, whereas the binary field has this one-to-one mapping convenience. In prime field Fp, common reduction methods include Barrett reduction, Montgomery reduction, and special reduction methods for specific finite fields such as Mersenne-31 or Goldilocks-64. In binary field F2k, commonly used reduction methods include special reductions (as used in AES), Montgomery reductions (as used in POLYVAL), and recursive reductions (such as Tower). The paper "Exploring the Design Space of Prime Field vs. Binary Field ECC-Hardware Implementations" points out that binary fields do not require carry in addition and multiplication operations, and squaring operations in binary fields are very efficient because they follow the simplified rule (X + Y)² = X² + Y².
As shown in Figure 1, a 128-bit string can be interpreted in various ways within the context of binary fields. It can be viewed as a unique element in a 128-bit binary field, or parsed as two 64-bit tower field elements, four 32-bit tower field elements, 16 eight-bit tower field elements, or 128 F2 field elements. This flexibility in representation requires no computational overhead; it is merely a typecast of the bit string, which is a very interesting and useful property. Additionally, small field elements can be packed into larger field elements without incurring extra computational overhead. The Binius protocol leverages this feature to enhance computational efficiency. Furthermore, the paper "On Efficient Inversion in Tower Fields of Characteristic Two" discusses the computational complexity of multiplication, squaring, and inversion operations in n-bit tower binary fields (which can be decomposed into m-bit subfields).
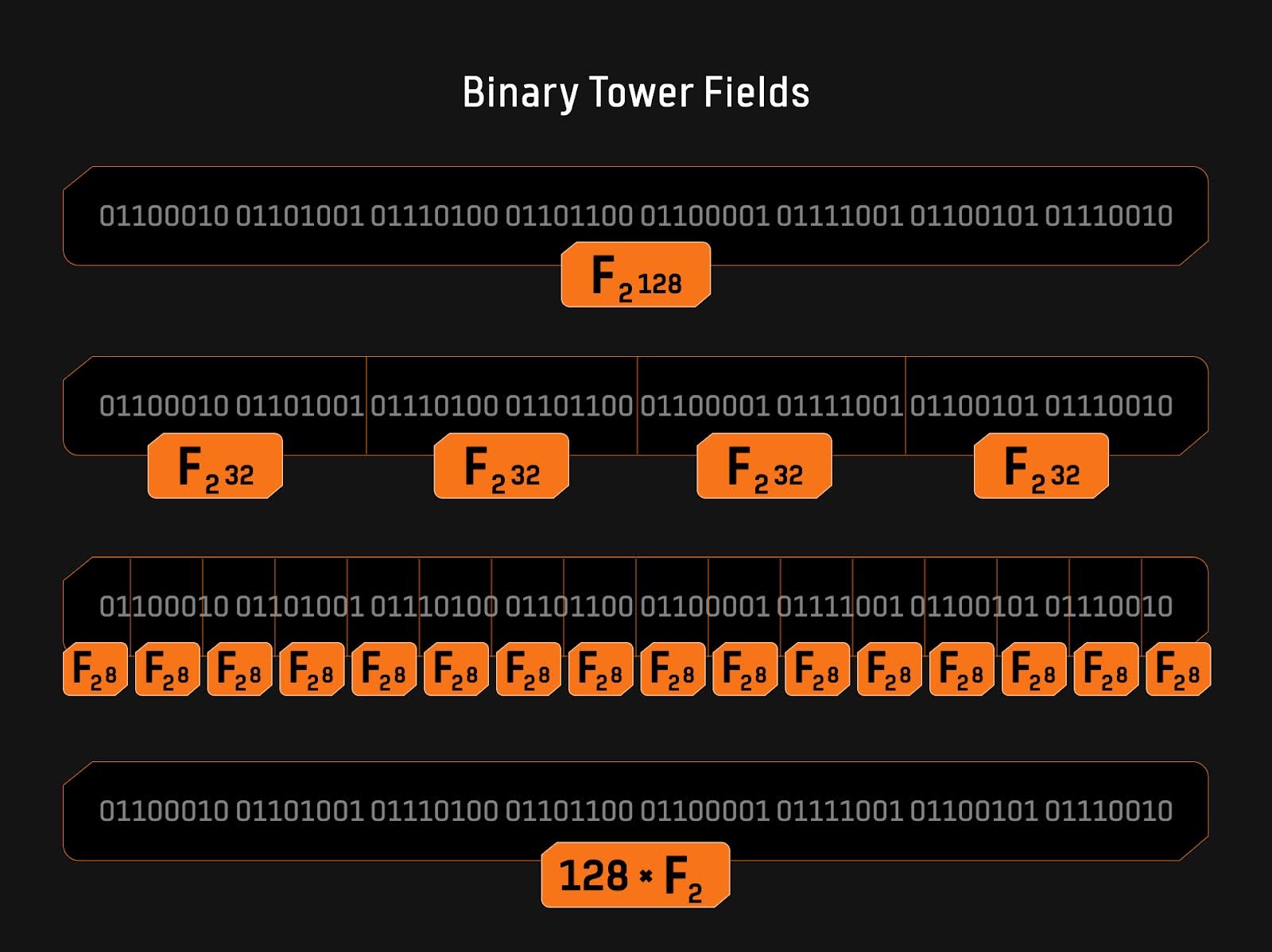
Figure 1: Tower-based Binary Field

2.2 PIOP: Adapted HyperPlonk Product and PermutationCheck—Applicable to Binary Fields
The PIOP design in the Binius protocol draws from HyperPlonk and employs a series of core checking mechanisms to verify the correctness of polynomials and multivariable sets. These core checks include:
GateCheck: Verifies whether the confidential witness ω and public input x satisfy the circuit operation relationship C(x,ω)=0 to ensure the circuit operates correctly.
PermutationCheck: Verifies whether the evaluation results of two multivariable polynomials f and g on the Boolean hypercube satisfy the permutation relation f(x) = f(π(x)), ensuring the consistency of polynomial variable arrangements.
LookupCheck: Verifies whether the evaluation of the polynomial is within a given lookup table, i.e., f(Bµ) ⊆ T(Bµ), ensuring certain values fall within a specified range.
MultisetCheck: Checks whether two multivariable sets are equal, i.e., {(x1,i,x2,)}i∈H={(y1,i,y2,)}i∈H, ensuring consistency among multiple sets.
ProductCheck: Detects whether the evaluation of a rational polynomial on the Boolean hypercube equals a declared value ∏x∈Hµ f(x) = s, ensuring the correctness of polynomial products.
ZeroCheck: Verifies whether a multivariable polynomial is zero at any point on the Boolean hypercube, ∏x∈Hµ f(x) = 0, ∀x ∈ Bµ, ensuring the distribution of the polynomial's zeros.
SumCheck: Checks whether the sum of a multivariable polynomial equals a declared value ∑x∈Hµ f(x) = s. By transforming the evaluation problem of a multivariable polynomial into a univariate polynomial evaluation, it reduces the computational complexity for the verifier. Additionally, SumCheck allows for batching, constructing linear combinations to achieve batch processing of multiple sum verification instances through the introduction of random numbers.
BatchCheck: Based on SumCheck, verifies the correctness of evaluations of multiple multivariable polynomials to improve protocol efficiency.
Although Binius shares many similarities with HyperPlonk in protocol design, it makes improvements in the following three areas:
ProductCheck Optimization: In HyperPlonk, ProductCheck requires the denominator U to be non-zero everywhere on the hypercube, and the product must equal a specific value; Binius simplifies this check by specializing that value to 1, thereby reducing computational complexity.
Handling of Division by Zero: HyperPlonk fails to adequately address division by zero cases, leading to an inability to assert the non-zero status of U on the hypercube; Binius correctly handles this issue, allowing ProductCheck to continue processing even when the denominator is zero, permitting generalization to any product value.
Cross-Column PermutationCheck: HyperPlonk lacks this functionality; Binius supports PermutationCheck across multiple columns, enabling it to handle more complex polynomial arrangement scenarios.
Thus, Binius enhances the flexibility and efficiency of the protocol through improvements to the existing PIOPSumCheck mechanism, particularly providing stronger functional support when dealing with more complex multivariable polynomial verifications. These improvements not only address the limitations in HyperPlonk but also lay the groundwork for future proof systems based on binary fields.
2.3 PIOP: New Multilinear Shift Argument—Applicable to Boolean Hypercube
In the Binius protocol, the construction and handling of virtual polynomials is one of the key technologies, effectively generating and manipulating polynomials derived from input handles or other virtual polynomials. The following are two key methods:
Packing: This method optimizes operations by packing smaller elements from adjacent positions in lexicographic order into larger elements. The Pack operator operates on blocks of size 2κ and combines them into a single element in a higher-dimensional field. Through Multilinear Extension (MLE), this virtual polynomial can be efficiently evaluated and processed, transforming function t into another polynomial, thereby enhancing computational performance.
Shift Operator: The shift operator rearranges elements within blocks, performing cyclic shifts based on a given offset o. This method applies to blocks of size 2b, with each block executing shifts according to the offset. The shift operator is defined by detecting the support of the function, ensuring consistency and efficiency when processing virtual polynomials. The complexity of evaluating this construction grows linearly with block size, making it particularly suitable for handling large datasets or high-dimensional scenarios in the Boolean hypercube.
2.4 PIOP: Adapted Lasso Lookup Argument—Applicable to Binary Fields
The Lasso protocol allows the prover to commit to a vector a ∈ Fm and prove that all its elements exist in a pre-specified table t ∈ Fn. Lasso unlocks the concept of "lookup singularities" and can be applied to multilinear polynomial commitment schemes. Its efficiency is reflected in the following two aspects:
Proof Efficiency: For m lookups in a table of size n, the prover only needs to commit to m+n field elements. These field elements are small and all lie within the set {0,…,m}. In commitment schemes based on multiple exponentiations, the prover's computational cost is O(m + n) group operations (such as elliptic curve point addition), plus the evaluation cost of whether the multilinear polynomial is a table element on the Boolean hypercube.
No Need to Commit to Large Tables: If the table t is structured, there is no need to commit to it, allowing for the handling of extremely large tables (such as 2^128 or larger). The prover's runtime is only related to the accessed table entries. For any integer parameter c > 1, the main cost for the prover is the proof size, with the committed field elements being 3·c m + c·n1/c. All these field elements are small, lying within the set {0,…,max{m,n1/c,q} − 1}, where q is the maximum value in a.
The Lasso protocol consists of the following three components:
Virtual Polynomial Abstraction for Large Tables: Achieves operations on large tables by combining virtual polynomials, ensuring efficient lookups and processing within the table.
Small Table Lookup: The core of Lasso is small table lookup, serving as the core construction of the virtual polynomial protocol, using offline memory detection to verify whether the evaluation of a virtual polynomial on the Boolean hypercube is a subset of the evaluation of another virtual polynomial. This lookup process reduces to the task of multiset detection.
Multiset Check: Lasso introduces a virtual protocol to perform multiset checks, verifying whether the elements of two sets are equal or meet specific conditions.
The Binius protocol adapts Lasso for operations in binary fields, assuming the current field is a prime field of large characteristic (far greater than the length of the column being looked up). Binius introduces a multiplicative version of the Lasso protocol, requiring the prover and verifier to jointly increment the protocol's "memory count" operation, not by simply incrementing by 1, but by using multiplicative generators in the binary field. However, this multiplicative adaptation introduces more complexity; unlike the increment operation, multiplicative generators do not increment in all cases, and there exists a single orbit at 0, which could become a point of attack. To prevent this potential attack, the prover must commit to a read count vector that is non-zero everywhere to ensure the security of the protocol.
2.5 PCS: Adapted Brakedown PCS—Applicable to Small-Field
The core idea behind constructing BiniusPCS is packing. The Binius paper provides two Brakedown polynomial commitment schemes based on binary fields: one instantiates using concatenated codes; the other employs block-level encoding techniques, supporting the standalone use of Reed-Solomon codes. The second Brakedown PCS scheme simplifies the proof and verification processes, although the proof size is slightly larger than the first, the simplifications and implementation advantages make this trade-off worthwhile.
Binius polynomial commitments primarily utilize small field polynomial commitments with extended field evaluations, small field universal constructions, and block-level encoding with Reed-Solomon code techniques.
Small Field Polynomial Commitments with Extended Field Evaluations: The commitments in the Binius protocol are polynomial commitments on the small field K, evaluated in a larger extended field L/K. This method ensures that each multilinear polynomial t(X0,…,Xℓ−1) belongs to the field K[X0,…,Xℓ−1], while the evaluation points can lie in the larger extended field L. The commitment scheme is specifically designed for small field polynomials and can query in the extended field while ensuring the security and efficiency of the commitments.
Small Field Universal Construction: The small field universal construction ensures that the extended field L is sufficiently large to support secure evaluations by defining parameters ℓ, field K, and its associated linear block code C. To enhance security while maintaining computational efficiency, the protocol guarantees the robustness of commitments by leveraging the properties of the extended field and encoding polynomials using linear block codes.
Block-Level Encoding and Reed-Solomon Codes: For polynomials with a field smaller than the linear block code alphabet, Binius proposes a block-level encoding scheme. Through this scheme, even polynomials defined in small fields (such as F2) can be efficiently committed using Reed-Solomon codes with larger alphabets, such as F216. Reed-Solomon codes are chosen for their efficiency and maximum distance separability properties. This scheme simplifies operational complexity by packing messages and encoding them row by row, followed by committing using a Merkle tree. Block-level encoding allows for efficient commitments of small field polynomials without incurring the high computational overhead typically associated with large fields, making it feasible to commit polynomials in small fields like F2 while maintaining computational efficiency in proof generation and verification.
3 Optimization Considerations
To further enhance the performance of the Binius protocol, this paper proposes four key optimization points:
GKR-based PIOP: For binary field multiplication, replacing the Lasso Lookup algorithm in the Binius paper with the GKR protocol can significantly reduce the commitment overhead of Binius;
ZeroCheck PIOP Optimization: Balancing the computational overhead between the Prover and Verifier to make the ZeroCheck operation more efficient;
Sumcheck PIOP Optimization: Optimizing the small field Sumcheck to further reduce the computational burden on small fields;
PCS Optimization: Reducing proof size through FRI-Binius optimization, improving the overall performance of the protocol.
3.1 GKR-based PIOP: Binary Field Multiplication Based on GKR
The Binius paper introduces a lookup-based scheme aimed at achieving efficient binary field multiplication. The binary field multiplication algorithm adapted from the Lasso lookup argument relies on the linear relationship between lookups and addition operations, which are proportional to the number of limbs in a single word. While this algorithm optimizes multiplication to some extent, it still requires auxiliary commitments that are linearly related to the number of limbs.
The core idea of the GKR (Goldwasser-Kalai-Rothblum) protocol is that the Prover (P) and Verifier (V) reach consensus on a layered arithmetic circuit over a finite field F. Each node of this circuit has two inputs for computing the desired function. To reduce the computational complexity for the Verifier, the protocol uses the SumCheck protocol to progressively simplify statements about the circuit output gate values into lower-level gate value statements until the statement is ultimately simplified to one about the inputs. This way, the Verifier only needs to check the correctness of the circuit inputs.
The GKR-based integer multiplication algorithm transforms the check of "whether two 32-bit integers A and B satisfy A·B =? C" into "check whether (gA)B =? gC holds," significantly reducing commitment overhead with the help of the GKR protocol. Compared to the previous Binius lookup scheme, the GKR-based binary field multiplication requires only one auxiliary commitment and becomes more efficient by reducing the overhead of Sumchecks, especially in scenarios where Sumcheck operations are cheaper than commitment generation. As Binius optimizations progress, GKR-based multiplication gradually becomes an effective way to reduce the commitment overhead of binary field polynomials.
3.2 ZeroCheck PIOP Optimization: Balancing Computational Overhead Between Prover and Verifier
The paper "Some Improvements for the PIOP for ZeroCheck" adjusts the workload distribution between the Prover (P) and Verifier (V), proposing various optimization schemes to balance costs. This work explores different configurations of k values, achieving a cost balance between the Prover and Verifier, particularly in reducing data transmission and lowering computational complexity.
Reducing Data Transmission from the Prover: By shifting part of the workload to the Verifier V, the amount of data sent by the Prover P is reduced. In the i-th round, the Prover P needs to send vi+1(X) to the Verifier V, where X=0,…,d + 1. The Verifier V checks the following equation to verify the correctness of the data:
vi = vi+1(0) + vi+1(1).
Optimization Method: The Prover P can choose not to send vi+1(1) but instead let the Verifier V compute this value by:
vi+1(1) = vi − vi+1(0).
Additionally, in the 0-th round, the honest Prover P always sends v1(0) = v1(1) = 0, meaning no evaluation calculations are needed, significantly reducing computational and transmission costs to d2n−1CF + (d + 1)2n−1CG.
Reducing the Number of Evaluation Points for the Prover: In the i-th round of the protocol, the Verifier has already sent a sequence of values r =(r0,…,ri−1) in the previous i rounds. The current protocol requires the Prover (P) to send the polynomial
vi+1(X) = ∑ δˆn(α,(r,X,x))C(r,X,x).x∈H −−1
Optimization Method: The Prover P sends the following polynomial, where the relationship between these two functions is:
vi(X) = vi′(X)·δi+1((α0,…,αi),(r,X))
where δˆi+1 is completely known to the Verifier since it has α and r. The benefit of this modification is that vi′(X) has a degree one less than vi(X), meaning the Prover needs to evaluate fewer points. Thus, the main protocol changes occur in the checking phase between rounds.
Furthermore, optimizing the original constraint vi = vi+1(0) + vi+1(1) to (1−αi)vi′+1(0) + αivi′+1(1) = vi′(X) reduces the data the Prover needs to evaluate and send, further decreasing the amount of transmitted data. Computing δˆn−i−1 is also more efficient than computing δˆn. With these two improvements, costs are reduced to approximately: 2n−1(d− 1)CF + 2n−1dCG. In the common case of d=3, these optimizations reduce costs by a factor of 5/3.
Algebraic Interpolation Optimization: For an honest Prover, C(x0,…,xn−1) is zero on Hn and can be expressed as: C(x0,…,xn-1)= ∑xi(xi-1)Qi(x0,…,xn-1). Although Qi is not unique, an ordered decomposition can be constructed through polynomial long division: starting from Rn=C, successively dividing by xi(xi−1) to compute Qi and Ri, where R0 is the multilinear extension of C on Hn, and it is assumed to be zero. Analyzing the degree of Qi, it can be concluded that: for j> i, Qj has the same degree as C; for j = i, the degree decreases by 2; for j < i, the degree is at most 1. Given the vector r = (r0,…,ri), Qj(r,X) is multilinear for all j ≤ i. Additionally, 1) Qj(r,X) is the unique multilinear polynomial equal to C(r,X) on Hn−i. For any X and x ∈ Hn−i−1, it can be expressed as:
C(r,X,x) − Qi(r,X,x) = X(X − 1)Qi+1(r,X,x)
Thus, in each round of the protocol, only one new Q is introduced, and its evaluation value can be derived from C and the previous Q, achieving interpolation optimization.
3.3 Sumcheck PIOP Optimization: Small Field-Based Sumcheck Protocol
The STARKs scheme implemented by Binius has very low commitment overhead, making the prover bottleneck no longer the PCS, but rather the sum-check protocol. Ingonyama proposed an improvement scheme for the small field-based Sumcheck protocol in 2024, corresponding to the Algo3 and Algo4 algorithms in Figure 2, and open-sourced the implementation code. Algorithm 4 focuses on merging the Karatsuba algorithm into Algorithm 3 to minimize the number of extended field multiplications at the cost of additional base field multiplications, thus performing better when extended field multiplications are significantly more expensive than base field multiplications.
- Impact of Switching Rounds and Improvement Factor
The improvements to the small field-based Sumcheck protocol focus on the choice of the switching round t. The switching round refers to the point in time when the optimized algorithm switches back to the naive algorithm. Experiments in the paper show that at the optimal switching point, the improvement factor reaches its maximum, followed by a parabolic trend. If this switching point is exceeded, the performance advantage of the optimized algorithm diminishes, and efficiency declines. This is due to the higher time ratio of base field multiplications to extended field multiplications on small fields, making it crucial to switch back to the naive algorithm at the appropriate time.
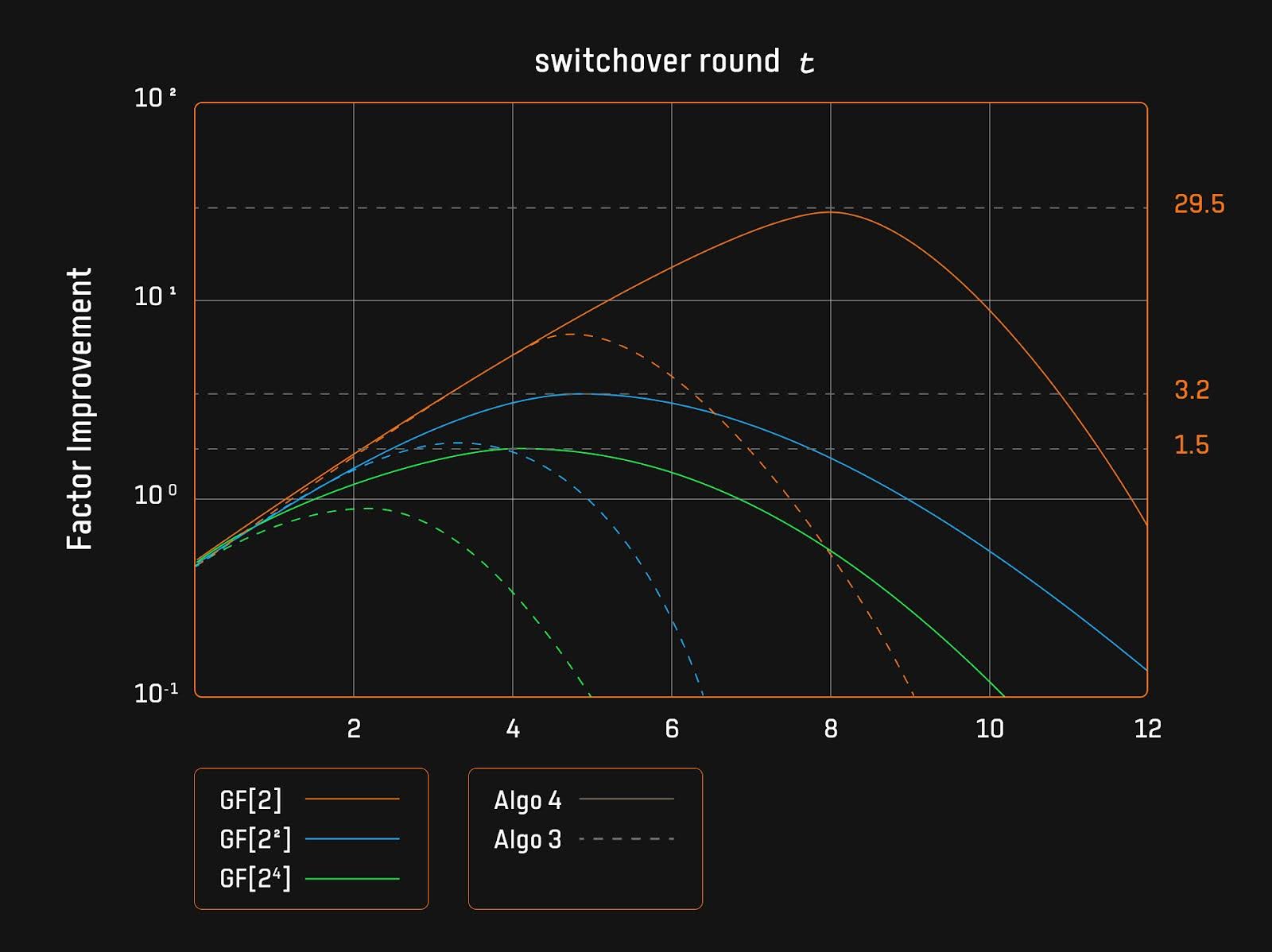
Figure 2: Relationship Between Switching Rounds and Improvement Factor
For specific applications, such as those involving Cubic Sumcheck (d = 3), the small field-based Sumcheck protocol achieves an order of magnitude improvement over the naive algorithm. For example, in the case of the base field being GF[2], the performance of Algorithm 4 is nearly 30 times higher than that of the naive algorithm.
- Impact of Base Field Size on Performance
Experimental results in the paper indicate that smaller base fields (such as GF[2]) allow the optimized algorithm to show more significant advantages. This is because the time ratio of extended field to base field multiplications is higher on smaller base fields, leading to a higher improvement factor for the optimized algorithm under these conditions.
- Optimization Benefits of the Karatsuba Algorithm
The Karatsuba algorithm demonstrates significant effects in enhancing the performance of the small field-based Sumcheck. For the base field GF[2], the peak improvement factors for Algorithms 3 and 4 are 6 and 30, respectively, indicating that Algorithm 4 is five times more efficient than Algorithm 3. The Karatsuba optimization not only improves runtime efficiency but also optimizes the switching points of the algorithms, achieving the best performance at t=5 for Algorithm 3 and t=8 for Algorithm 4.
- #### Improvement in Memory Efficiency
The small field-based Sumcheck protocol not only improves runtime but also demonstrates significant advantages in memory efficiency. Algorithm 4 has a memory requirement of O(d·t), while Algorithm 3 has a memory requirement of O(2d·t). When t=8, Algorithm 4 requires only 0.26MB of memory, whereas Algorithm 3 requires 67MB to store the products in the base field. This makes Algorithm 4 more adaptable in memory-constrained devices, especially suitable for resource-limited client proof environments.
3.4 PCS Optimization: FRI-Binius Reduces Binius Proof Size
A major drawback of the Binius protocol is its relatively large proof size, which scales with the square root of the witness size at O(√N). This square root-sized proof is a limitation compared to more efficient systems. In contrast, logarithmic (polylogarithmic) proof sizes are crucial for achieving truly "succinct" verifiers, as validated in advanced systems like Plonky3, which achieves logarithmic proof sizes through advanced techniques like FRI.
The paper "Polylogarithmic Proofs for Multilinears over Binary Towers," abbreviated as FRI-Binius, implements a binary field FRI folding mechanism, bringing four innovations:
Flattened Polynomials: The initial multilinear polynomial is transformed into a novel polynomial basis with low code height (LCH).
Vanishing Subspace Polynomials: Used to perform FRI over the coefficient field, achieving FFT-like decomposition through additive NTT (Number Theoretic Transform).
Algebraic Basis Packing: Supports efficient packing of information in the protocol, allowing the removal of embedding overhead.
Ring-Swapping SumCheck: A novel SumCheck method that optimizes performance using ring-swapping techniques.
The core idea of the binary field FRI-Binius polynomial commitment scheme (PCS) is that the FRI-Binius protocol operates by packaging the initial binary field multilinear polynomial (defined over F2) into a multilinear polynomial defined over a larger field K.
In the binary field-based FRI-Binius PCS, the process is as follows:
Commitment Phase: The commitment to an ℓ-variable multilinear polynomial (defined over F2) is transformed into a commitment to a packed ℓ′-variable multilinear polynomial (defined over F2128), reducing the number of coefficients by a factor of 128.
Evaluation Phase: The Prover and Verifier engage in ℓ′ rounds of cross-ring-switching SumCheck and FRI interactive proofs (IOPP):
– The FRI open proof occupies most of the proof size.
– The Prover's SumCheck cost is similar to the SumCheck cost on conventional large fields.
– The Prover's FRI cost is the same as the FRI cost on conventional large fields.
– The Verifier receives 128 elements from F2128 and performs 128 additional multiplications.
With the help of FRI-Binius, the proof size of Binius can be reduced by an order of magnitude. This brings the proof size of Binius closer to that of state-of-the-art systems while maintaining compatibility with binary fields. The FRI folding technique tailored for binary fields, combined with algebraic packing and SumCheck optimizations, enables Binius to generate more concise proofs while maintaining efficient verification.
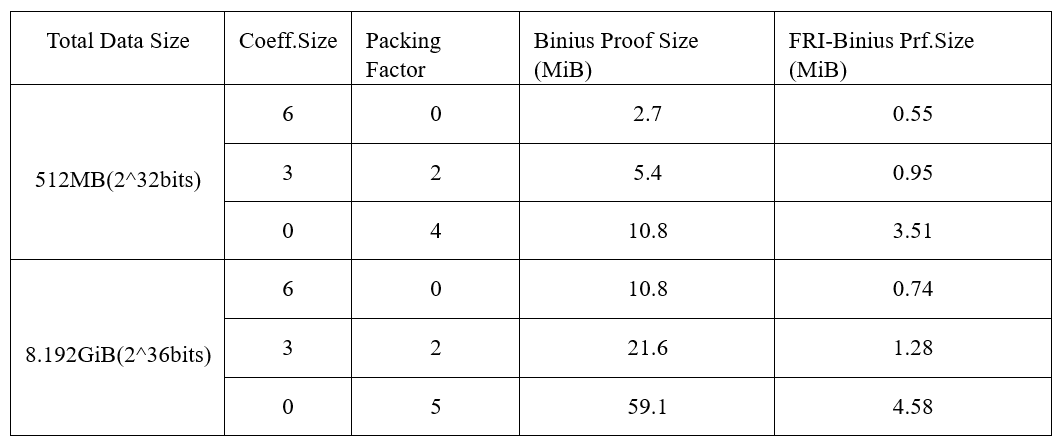
Table 2: Binius vs. FRI-Binius Proof Size
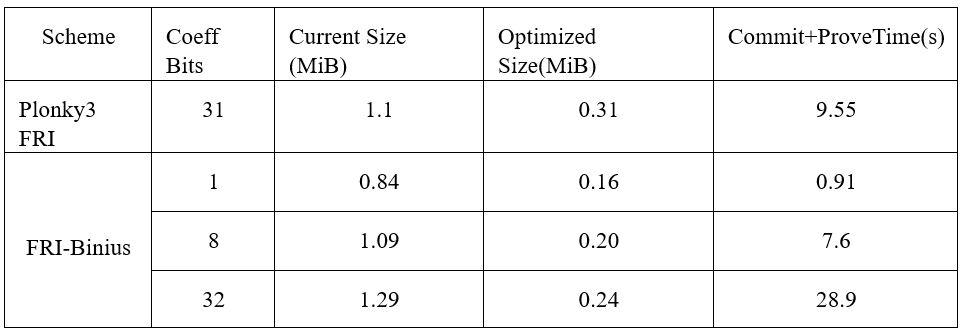
Table 3: Plonky3 FRI vs. FRI-Binius
4 Conclusion
The entire value proposition of Binius is that it can use the smallest power-of-two fields for witnesses, allowing for the selection of field size based solely on requirements. Binius is a collaborative design solution that utilizes "hardware, software, and FPGA-accelerated Sumcheck protocols" to quickly prove with very low memory usage. Proof systems like Halo2 and Plonky3 have four key steps that occupy most of the computational load: generating witness data, committing to witness data, vanishing argument, and opening proof. Taking the Keccak and Grøstl hash functions in Plonky3 and Binius as examples, the computational load of these four key steps is shown in Figure 3:
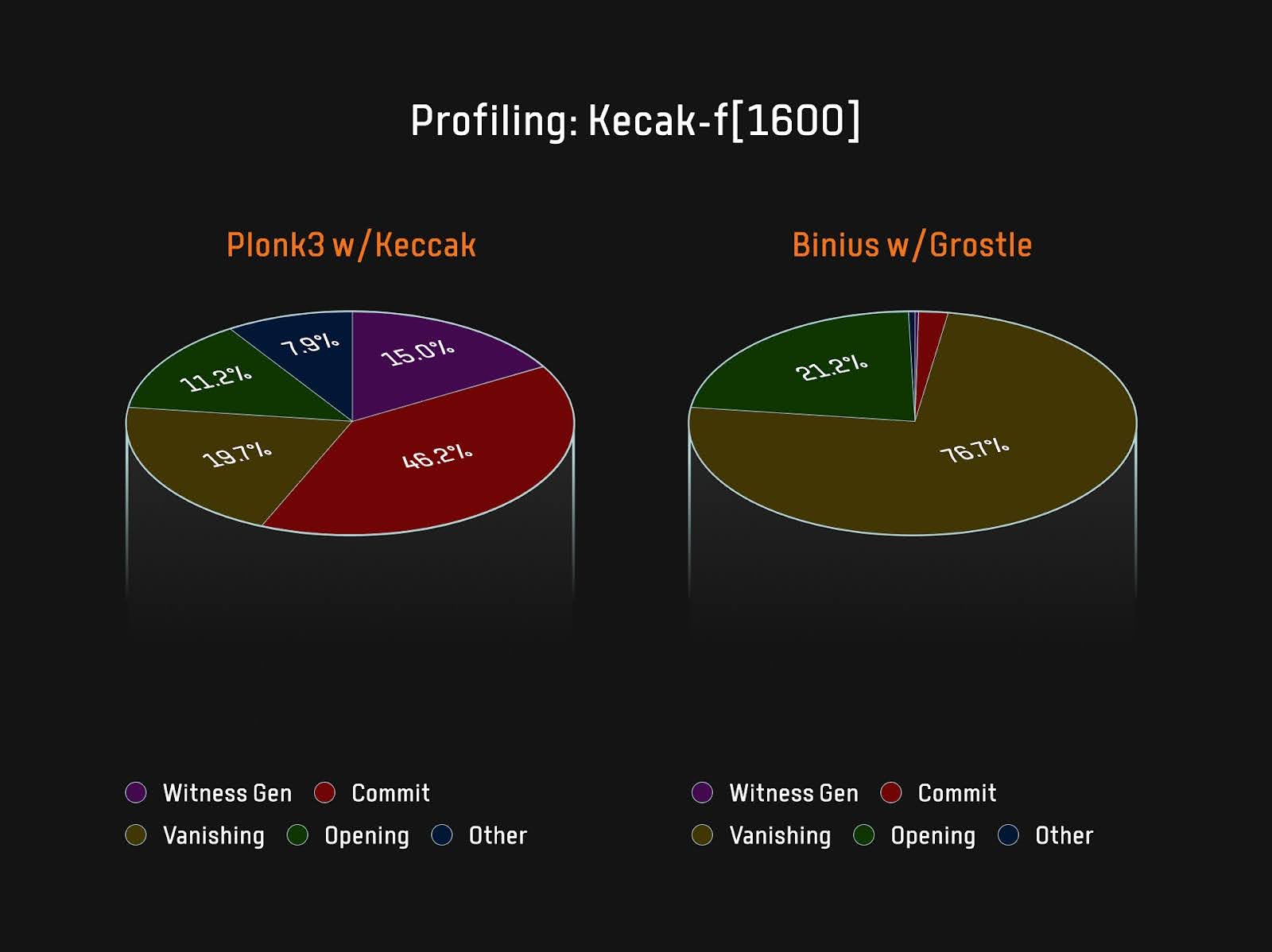
Figure 3: Smaller Commit Cost
It can be seen that Binius has essentially eliminated the commitment bottleneck for the Prover, with the new bottleneck being the Sumcheck protocol. The issues of numerous polynomial evaluations and field multiplications in the Sumcheck protocol can be efficiently addressed with dedicated hardware. The FRI-Binius scheme, as a variant of FRI, offers a very attractive option—eliminating embedding overhead from the field proof layer without causing a surge in costs for the aggregate proof layer. Currently, the Irreducible team is developing its recursive layer and announced a collaboration with the Polygon team to build a Binius-based zkVM; JoltzkVM is transitioning from Lasso to Binius to improve its recursive performance; the Ingonyama team is implementing an FPGA version of Binius.
References
2024.04 Binius Succinct Arguments over Towers of Binary Fields
2024.07 FRI-Binius Polylogarithmic Proofs for Multilinears over Binary Towers
2024.08 Integer Multiplication in Binius: GKR-based approach
2024.06 zkStudyClub - FRI-Binius: Polylogarithmic Proofs for Multilinears over Binary Towers
2024.04 ZK11: Binius: a Hardware-Optimized SNARK - Jim Posen
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。



