In the series of articles on advanced formal verification of zero-knowledge proofs, we have discussed how to verify ZK instructions and conducted a deep analysis of two ZK vulnerabilities.

As shown in the public report (https://skynet.certik.com/projects/zkwasm) and the code repository (https://github.com/CertiKProject/zkwasm-fv), by formally verifying each zkWasm instruction, we have identified and fixed every vulnerability, thus being able to fully verify the technical security and correctness of the entire zkWasm circuit.

Although we have demonstrated the process of verifying a zkWasm instruction and introduced the preliminary concepts of the related project, readers familiar with formal verification may be more interested in understanding the unique aspects of verifying zkVM compared to other smaller ZK systems or other types of bytecode VMs. In this article, we will delve into some technical points encountered in verifying the zkWasm memory subsystem. Memory is the most unique part of zkVM, and handling this is crucial for the verification of all other zkVM components.

Formal Verification: Virtual Machine (VM) vs. ZK Virtual Machine (zkVM)

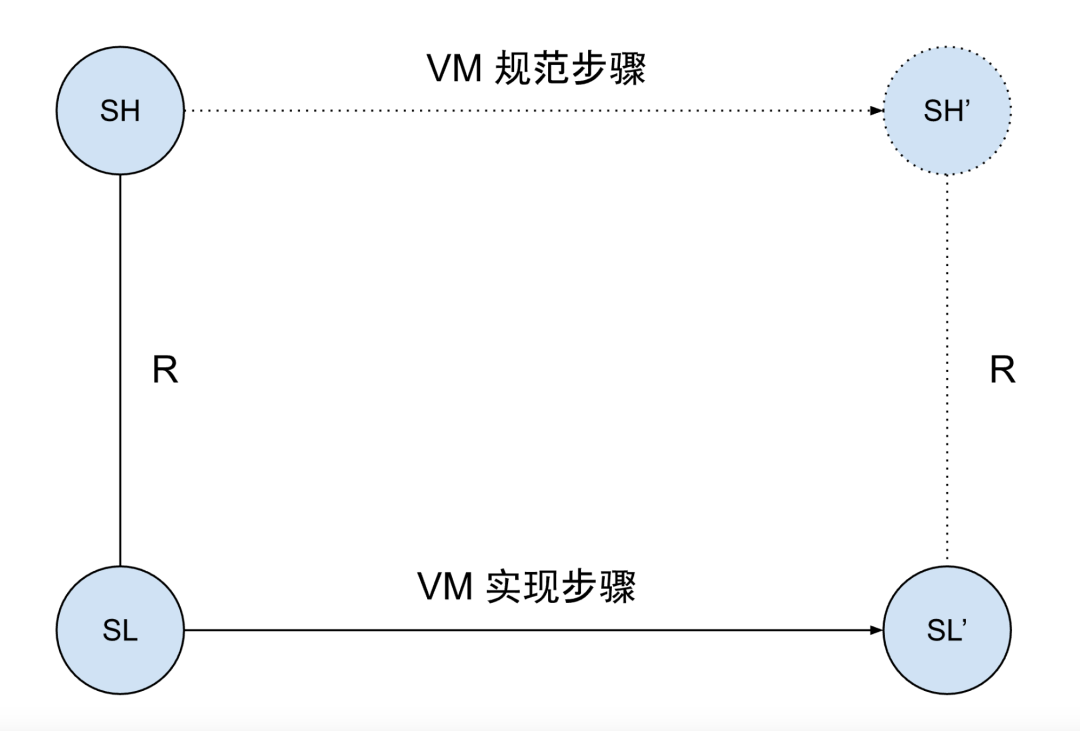
Our ultimate goal is to verify the correctness of zkWasm, which is similar to proving the correctness theorem of a regular bytecode interpreter (VM, such as the EVM interpreter used by Ethereum nodes). That is, every execution step of the interpreter corresponds to a legitimate step based on the language's operational semantics. As shown in the following figure, if the data structure's current state of the bytecode interpreter is SL, and this state is marked as state SH in the high-level specification of the Wasm machine, then when the interpreter steps to state SL', there must exist a corresponding legitimate high-level state SH', and the Wasm specification dictates that SH must step to SH'.

Similarly, zkVM also has a similar correctness theorem: each new row in the zkWasm execution table corresponds to a legitimate step based on the language's operational semantics. As shown in the following figure, if the current state of a row in the execution table is SR, and this state is represented as state SH in the high-level specification of the Wasm machine, then the next row state SR' in the execution table must correspond to a high-level state SH', and the Wasm specification dictates that SH must step to SH'.

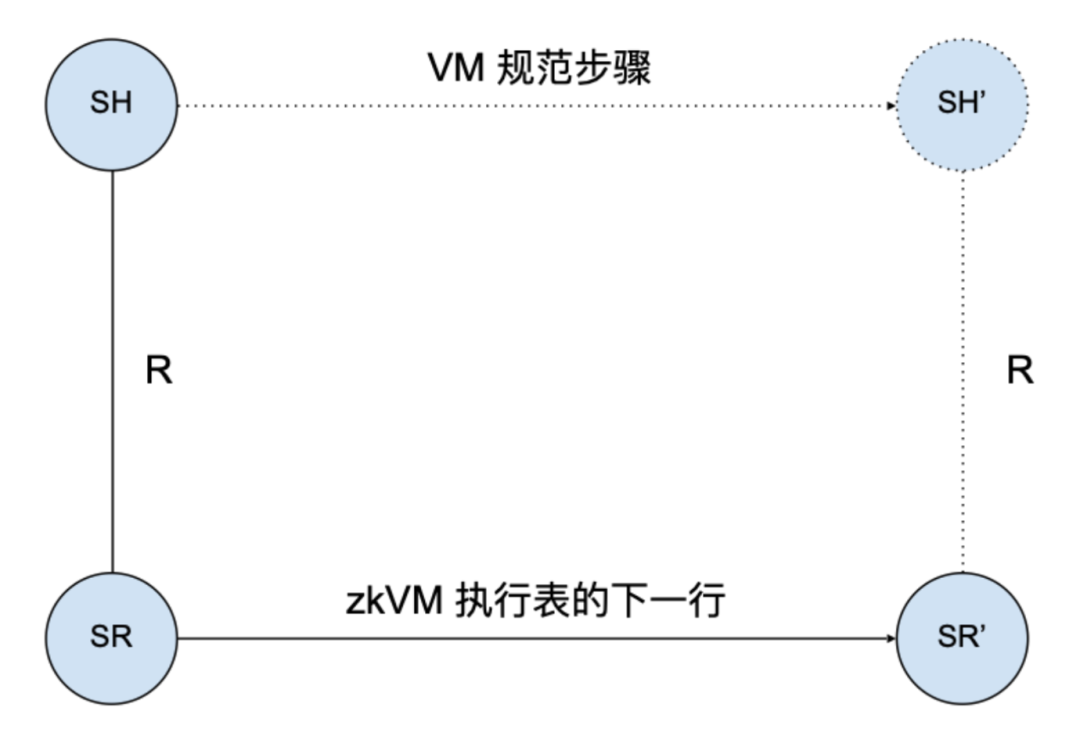
It can be seen that in both VM and zkVM, the high-level states and the specification of Wasm steps are consistent, so previous verification experience with programming language interpreters or compilers can be leveraged. The uniqueness of zkVM verification lies in the data structure types that constitute the system's low-level states.

First, as we have discussed in previous articles, the zk prover essentially involves integer operations modulo large prime numbers, while the Wasm specification and regular interpreters handle 32-bit or 64-bit integers. Most of the content implemented by zkVM involves this, so corresponding adjustments are needed in the verification process. However, this is a "local" issue: as arithmetic operations need to be handled, each line of code becomes more complex, but the overall structure of the code and proof remains unchanged.

Another major difference is how to handle dynamically sized data structures. In a regular bytecode interpreter, memory, data stack, and call stack are implemented as mutable data structures, and similarly, the Wasm specification represents memory as a data type with get/set methods. For example, Geth's EVM interpreter has a Memory data type, which is implemented as a byte array representing physical memory and is written to and read from using Set32 and GetPtr methods to implement a memory storage instruction. In the correctness proof of this interpreter, after assigning specific memory in the interpreter to abstract memory in the specification, we prove that the high-level state and low-level state match, which is relatively straightforward.

However, for zkVM, the situation becomes more complex.

zkWasm Memory Table and Memory Abstraction Layer

In zkVM, the execution table has columns for fixed-size data (similar to registers in a CPU), but it cannot handle dynamically sized data structures, which are implemented through lookup tables. The zkWasm execution table has an EID column with values of 1, 2, 3, and so on, and there are two auxiliary tables, the memory table and the jump table, used to represent memory data and the call stack, respectively.

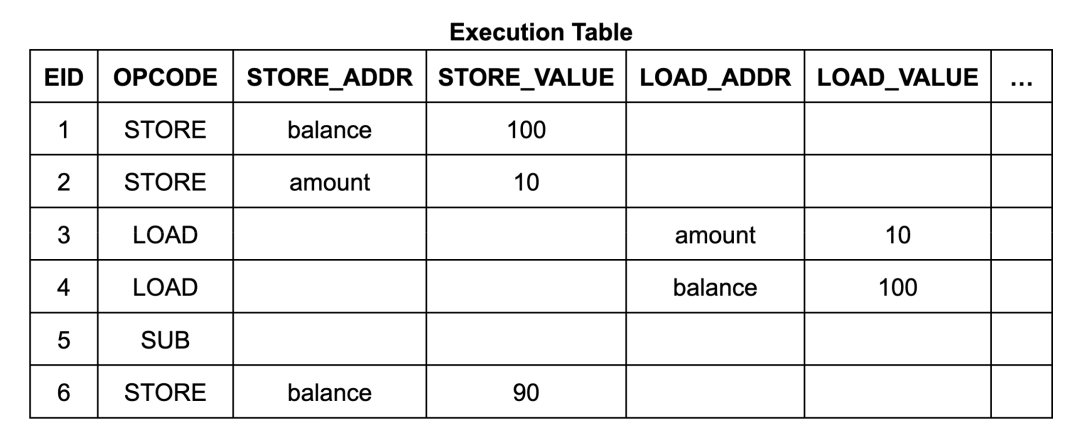
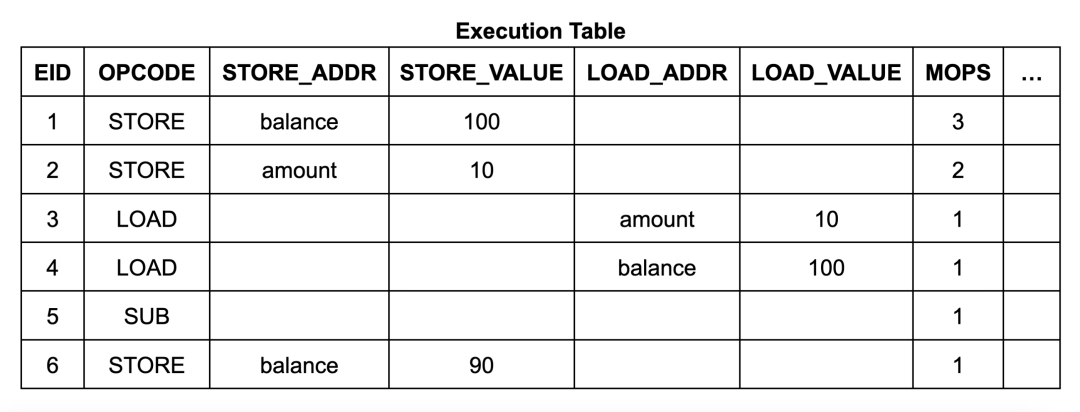
Here is an example of a withdrawal program implementation:

int balance, amount;void main () {balance = 100; amount = 10;balance -= amount; // withdraw}

The content and structure of the execution table are quite simple. It has 6 execution steps (EID1 to 6), each step lists its opcode, and if the instruction is a memory read or write, it also lists its address and data:

Each row in the memory table contains the address, data, start EID, and end EID. The start EID is the EID of the execution step that writes the data to the address, and the end EID is the EID of the next step that will write to the address. (It also includes a counter, which we will discuss in detail later.) For the Wasm memory read instruction circuit, it uses lookup constraints to ensure that there is a suitable entry in the table, such that the EID of the read instruction is within the range from start to end. (Similarly, each row in the jump table corresponds to a frame of the call stack, with each row labeled with the EID of the instruction that created it.)

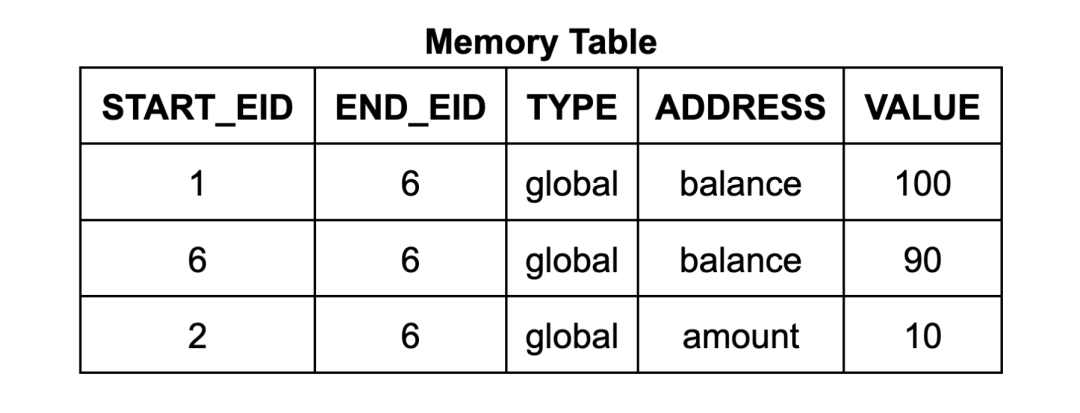
This memory system is quite different from a regular VM interpreter: the memory table is not a gradually updated mutable memory, but rather contains the entire history of all memory accesses in the execution trace. To simplify the programmer's work, zkWasm provides an abstraction layer, implemented through two convenient entry functions:

allocmemorytablelookupwrite_cell

and

allocmemorytablelookupread_cell

with the following parameters:

For example, the code implementing the memory storage instruction in zkWasm includes a call to the write alloc function:

let memorytablelookupheapwrite1 = allocator.allocmemorytablelookupwritecellwithvalue( "store write res1", constraintbuilder, eid, move || constantfrom!(LocationType::Heap as u64), move |meta| loadblockindex.expr(meta), // address move || constantfrom!(0), // is 32-bit move || constantfrom!(1), // (always) enabled ); let storevalueinheap1 = memorytablelookupheapwrite1.valuecell;

The alloc function is responsible for handling lookup constraints between tables and associating the current eid with memory table entries, as well as arithmetic constraints. Thus, programmers can treat these tables as regular memory, and after the code execution, the value of storevalueinheap1 has been assigned to the loadblock_index address.

Similarly, the memory read instruction uses the read_alloc function. In the example execution sequence above, each load instruction has a read constraint, each store instruction has a write constraint, and each constraint is satisfied by an entry in the memory table.

The structure of formal verification should correspond to the abstraction used in the software being verified, allowing the proof to follow the same logic as the code. For zkWasm, this means we need to verify the memory table circuit and the "alloc read/write cell" functions as a module, with an interface similar to mutable memory. With such an interface, the verification of each instruction circuit can be done in a similar way to a regular interpreter, while the additional ZK complexity is encapsulated in the memory subsystem module.

In the verification, we specifically implemented the idea that "the memory table can be seen as a mutable data structure." That is, we write a function memoryattype, which fully scans the memory table and constructs the corresponding address data mapping. (Here, the variable type takes on three different types of Wasm memory data: heap, data stack, and global variables.) Then, we prove that the memory constraints generated by the alloc function are equivalent to the data changes made by the set and get functions on the corresponding address data mapping. We can prove:

• For each eid, if the following constraint holds

memorytablelookupreadcelleidtypeoffsetvalue

then

get(memory_ateidtype)offset = Somevalue

• And if the following constraint holds

memorytablelookupwritecell eid type offset value

then

memoryat (eid+1) type = set (memoryat eid type) offset value

After this, the verification of each instruction can be based on the get and set operations on the address data mapping, similar to a non-ZK bytecode interpreter.

Memory Write Counting Mechanism in zkWasm

However, the simplified description above does not reveal all the contents of the memory table and jump table. Under the framework of zkVM, these tables may be manipulated by attackers, who can easily manipulate memory load instructions by inserting a row of data to return an arbitrary value.

For example, in a withdrawal program, an attacker has the opportunity to inject false data into the account balance by forging a $110 memory write operation before the withdrawal operation. This can be achieved by adding a row of data to the memory table and modifying the values of existing cells in the memory table and execution table. This would allow the attacker to perform a "free" withdrawal, as the account balance would still remain at $100 after the operation.

To ensure that the memory table (and jump table) only contains valid entries generated by actual memory write (and call and return) instructions, zkWasm employs a special counting mechanism to monitor the number of entries in the memory table. Specifically, the memory table has a dedicated column to continuously track the total number of memory write entries. Similarly, the execution table also includes a counter to count the expected number of memory write operations for each instruction. By setting an equality constraint, it ensures that these two counts are consistent. The logic of this approach is intuitive: each memory write operation is counted whenever it occurs, and there should be a corresponding record in the memory table. Therefore, attackers cannot insert any additional entries into the memory table.

The above logical statement is somewhat vague, and in the process of mechanized proof, it needs to be made more precise. First, we need to refine the statement of the previous memory write lemma. We define the function mopsateid_type, which counts the number of memory table entries with a given eid and type (most instructions will create 0 or 1 entry at an eid). The complete statement of this lemma has an additional premise, indicating that there are no false memory table entries:

If the following constraint holds

(memorytablelookupwritecelleidtypeoffsetvalue)

and the following additional constraint holds

(mops_ateidtype)=1

then

(memoryat(eid+1)type)=set(memoryateidtype)offsetvalue

This requires our verification to be more precise than the previous case. It is not sufficient to prove that the total number of memory table entries equals the total number of memory write operations in the execution from the equality constraint alone. To prove the correctness of instructions, we need to know that each instruction corresponds to the correct number of memory table entries. For example, we need to exclude the possibility of an attacker omitting a memory table entry for a certain instruction in the execution sequence and creating a malicious new memory table entry for another unrelated instruction. ```

To prove this, we adopt a top-down approach to restrict the number of memory table entries corresponding to a given instruction, which involves three steps. First, we estimate the expected number of entries to be created for the instructions in the execution sequence based on the instruction type. We denote the expected number of writes from the i-th step to the end of the execution as instructionsmopsi, and the corresponding number of entries in the memory table from the i-th instruction to the end of the execution as cummops(eidi). By analyzing the lookup constraints of each instruction, we can prove that the created entries are no less than expected, thus concluding that the entries created for each segment [i … numRows] tracked are no less than expected:

Lemma cummopsbound': forall n i, 0 ≤ i -> i + Z.ofnat n = etablenumRow -> MTable.cummops(etablevalueseidcelli)(maxeid+1)≥instructions_mops'in.

Secondly, if we can prove that the number of entries in the table is not more than expected, then it has exactly the correct number of entries, which is obvious.

Lemma cummopsequal' : forall n i, 0 ≤ i -> i + Z.ofnat n = etablenumRow -> MTable.cummops (etablevalues eidcell i) (maxeid+1) ≤ instructionsmops' i n ->MTable.cummops(etablevalueseidcelli)(maxeid+1)=instructionsmops'in.

Now, onto the third step. Our correctness theorem states that for any n, cummops and instructionsmops are always consistent in the table from the n-th row to the end:

Lemma cummopsequal : forall n, 0 = Z.ofnat n etablenumRow ->MTable.cummops(etablevalueseidcell(Z.ofnatn))(maxeid+1)=instructionsmops(Z.of_natn)

The verification is completed by inductively summarizing over n. The first row of the table is the equality constraint of zkWasm, indicating that the total number of entries in the memory table is correct, i.e., cummops 0 = instructionsmops 0. For the subsequent rows, the inductive hypothesis tells us:

cummopsn=instructionsmopsn

And we want to prove

cummops (n+1) = instructionsmops (n+1)

Note that

cummops n = mopsat n + cum_mops (n+1)

And

instructionsmops n = instructionmops n + instructions_mops (n+1)

Therefore, we can derive

mopsat n + cummops (n+1) = instructionmops n + instructionsmops (n+1)

Previously, we have proven that each instruction will create no less than the expected number of entries, for example

mopsat n ≥ instructionmops n.

So we can conclude

cummops (n+1) ≤ instructionsmops (n+1)

Here we need to apply the second lemma mentioned above.

Detailing the proof process in this manner is a typical feature of formal verification and is often the reason why verifying specific code segments takes longer than writing them. However, is it worth it? In this case, it is, as we did discover a critical error in the jump table counting mechanism during the proof process. The previous article detailed this error - in summary, the old version of the code counted both call and return instructions, and attackers could make space for forged jump table entries by adding extra return instructions in the execution sequence. While the incorrect counting mechanism may satisfy the intuition of counting every call and return instruction, the problem becomes apparent when we try to refine this intuition into more precise theorem statements.

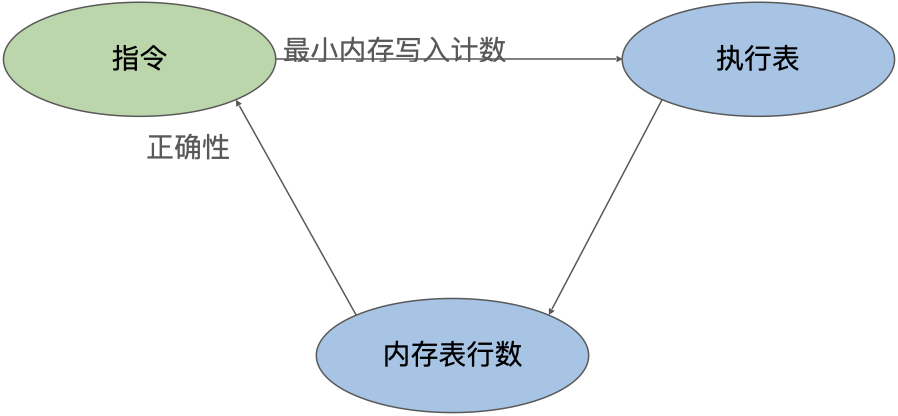
Modularizing the Proof Process

From the discussion above, we can see that there is a circular dependency between the proof of the circuit for each instruction and the proof of the counting column in the execution table. To prove the correctness of the instruction circuit, we need to reason about the memory writes within it; that is, we need to know the number of memory table entries at a specific EID and prove that the count of memory write operations in the execution table is correct, which in turn requires proving that each instruction has executed at least the minimum number of memory write operations.

Additionally, another factor to consider is that the zkWasm project is quite large, so the verification work needs to be modularized for multiple verification engineers to work on. Therefore, special attention is needed when deconstructing the proof of the counting mechanism. For example, for the LocalGet instruction, there are two theorems:

Theorem opcodemopscorrectlocalget : forall i, 0 = i -> etablevalues eidcell i > 0 -> opcodemopscorrect LocalGet i.

Theorem LocalGetOpcorrect : forall i st y xs, 0 = i -> etablevalues enabledcell i = 1 -> mopsatcorrect i -> etablevalues (opscell LocalGet) i = 1 -> staterel i st -> wasmstack st = xs -> (etablevalues offsetcell i) > 1 -> ntherror xs (Z.tonat (etablevalues offsetcell i - 1)) = Some y ->staterel(i+1)(updatestack(incriidst)(y::xs)).

The first theorem states that

opcodemopscorrect LocalGet i

which, when expanded, means that the instruction at the i-th row creates at least one memory table entry (the number 1 is specified in the zkWasm LocalGet opcode specification).

The second theorem is the complete correctness theorem for this instruction, which references

mopsatcorrect i

as a hypothesis, indicating that the instruction accurately creates a memory table entry.

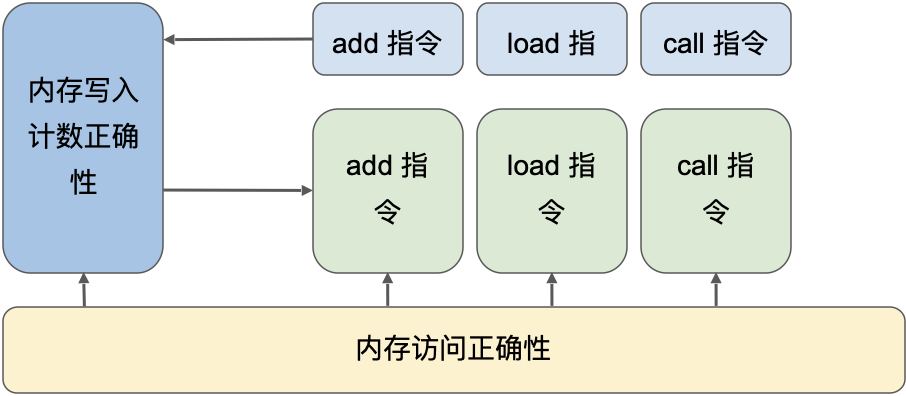
Verification engineers can independently prove these two theorems and then combine them with the proof of the execution table to establish the correctness of the entire system. It is worth noting that all proofs for individual instructions can be done at the level of read/write constraints without needing to understand the specific implementation of the memory table. Thus, the project is divided into three independently manageable parts.

Conclusion

Verifying the zkVM circuit line by line is not fundamentally different from verifying ZK applications in other domains, as they all require similar reasoning about arithmetic constraints. From a high-level perspective, verifying zkVM requires the use of many methods used in formal verification of programming language interpreters and compilers. The main difference here lies in the dynamically sized virtual machine state. However, by carefully constructing the verification structure to match the abstraction layer used in the implementation, the impact of these differences can be minimized, allowing each instruction to be independently and modularly verified based on the get-set interface, similar to a regular interpreter.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。